ブラックホールでは何が起きているのか
2014年4月、米科学誌Scienceに掲載された論文「量子ブラックホールのホログラム的記述の数値的検証」※１が世界の注目を集めています。その著者の一人、京都大学基礎物理学研究所の伊敷 吾郎（いしき・ごろう）特任助教は超弦（ちょうげん）理論の研究者です。
建築を学んでいた伊敷さんは、学部3年生のときに、その後の人生を決める1冊の本に出合いました。「その本には『宇宙現象のすべてを記述できる究極の理論―超弦理論が完成間近である。その理論を完成すべく、世界中の研究者が英知を結集している』と書いてあったように記憶しています。超弦理論というのはそんなにすごい理論なのか。勉強してみたい、と思いました」と伊敷さんは当時の衝撃を振り返ります。
今では、超弦理論の完成を目指す一人となった伊敷さん。「超弦理論は、まだまだわからないことが多い。まるで暗闇のなかで手探りをしているようだ」と感じるそうです。世界中の研究者が挑みながらもいまだに性質がつかみきれない「量子ブラックホール」。世界に先駆けて取り組んだ「量子重力効果」を考慮にいれたブラックホールに関する研究についてお話を伺いました。
一般相対論の限界
銀河や恒星、惑星の運動など宇宙で起こる現象は、アインシュタインの一般相対性理論でほとんど説明できます。ところが、一般相対論は、重力が非常に強く極度に曲がった時空では破綻してしまいます。たとえば、半径が非常に小さいブラックホールの中心付近や、まだ体積が非常に小さかった初期の宇宙などです。目に見えないようなミクロな世界は、一般相対論では説明できないのです。
曲がりの大きな時空で起こる現象を説明するには、ミクロな世界を支配する量子力学的な考えを入れる必要があります。「ある物理量になる確率がこのくらい、また違う物理量になる確率はこのくらい」という考え方をする「量子重力効果」を使います。すると、時空そのものが不確定性を持って揺らいでいる状態を数式で表せるようになります。
超弦理論の可能性
「量子重力効果」を扱える理論として有望視されているのが、1980年代に生まれた超弦理論です。これは力を粒子が媒介し、その粒子は非常に小さな「ひも（弦）」のようなふるまいをすると考える理論です。0次元の点ではなく、1次元のひもで考えるところが他の理論と決定的に違います。超弦理論を使えば、自然界で働く4つの力（重力、電磁力、強い力、弱い力）を統一的に扱えるのではないかと期待されています。
超弦理論はとても複雑な理論で、未知の部分が多く残されています。私たちは、「宇宙は4次元時空」と捉えています。ところが、超弦理論では、「宇宙は10（あるいは11）次元である」としないと矛盾が生じてしまいます。私たちが認識している4次元＋私たちが認識できていない6（あるいは7）次元で説明するというのです。
ところが、いまのところ超弦理論で定式化（方程式で書き表すこと）ができているのは、10次元の平坦な時空上の場合と、あるわずかに曲がった時空上の場合だけです。あらゆる曲がった時空の上で定式化できるという段階まで研究が進んでいないというのが実情です。
物理学者マルダセナの仮説は正しいのか
超弦理論でなくてもブラックホールを理解できるのではないかという画期的な考えを1997年にアルゼンチン出身のマルダセナ博士が発表しました※2。「ゲージ理論を使ってブラックホールを記述できる」という仮説です。
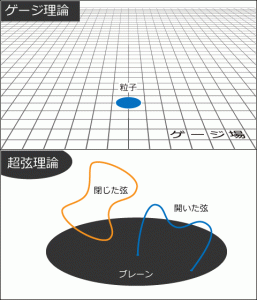
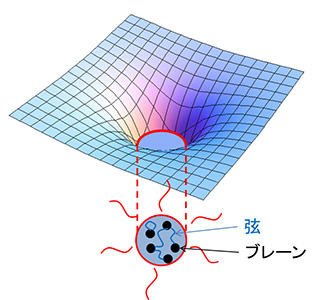
図1 マルダセナ博士は、ブラックホールのように極端に曲がった時空で起こる現象を、平らな時空上で厳密な数式（ゲージ理論）で表せると提唱した。2次元の平面上に3次元の立体像が浮かび上がることになぞらえ、これを「ホログラム的記述」と呼ぶ。「ブレーン」は弦や点の状態にある粒子の総称。
「ゲージ理論と超弦理論は等価性を持つ」ことを意味するこの仮説は、にわかには信じがたい側面を持っていました。なぜなら、ゲージ理論と超弦理論は多くの点で異なる理論だったからです。超弦理論が4つの力すべてを記述できるのに対して、ゲージ理論は重力を記述できません。また、超弦理論が10（あるいは11次元）なのに対し、ゲージ理論は1～4次元で記述されます。
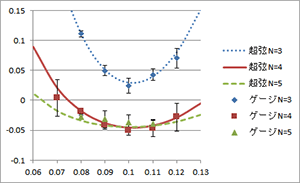
図2 温度とブラックホール質量の関係※3。縦軸はブラックホールの質量、横軸は温度を表している。Nは計算に使用したブラックホールの構成要素の数。これまでの研究はN＝17といった構成要素数の多いブラックホール（量子重力効果を無視できるほどの影響力しかもたないブラックホール）の研究のみだった。ゲージ理論を使った計算結果は、○△□で示される。3本の曲線は超弦理論を使った計算結果。○△□と曲線が良く一致していることが、ゲージ理論と超弦理論の等価性を裏付ける実証結果となった。N=3のような量子重力効果が非常に大きなパラメータでもよく一致している。超弦理論の計算をしたのは茨城大学の百武慶文准教授。伊敷さんは、京都大学の花田政範特定准教授とともにゲージ理論を使った数値解析を担当した。（図はHanada, Hyakutake, Ishiki, Nishimura 2014を元に作成）
一方で、この仮説に物理学者たちは大きな期待を寄せました。というのも、ゲージ理論は超弦理論よりはるかに理解が進んでいる理論だからです。もしこの仮説が本当ならば、ブラックホールなどの曲がった時空の理解が一気に進む可能性があります。
世界中でこの仮説を検証する研究が始まっています。いまのところ「この仮説は正しくない」という事例は見つかっていません。ただし、これまでの研究は比較的大きなブラックホール、つまり量子重力効果が無視できる領域の研究ばかりです。量子重力効果を含めると、超弦理論もゲージ理論も計算が非常に複雑になるため、多くの研究者が敬遠していたのです。
伊敷さんらは、「量子重力効果も考慮に入れなければ、マルダセナの仮説を本当の意味で裏づけたことにはならない」と考え、複雑な計算にコンピュータを駆使して挑戦しました。図2を見ると、ゲージ理論を使って計算したブラックホールの温度と時間の関係（グラフ中の15個のスポット）と、超弦理論から計算した3本の曲線がよく一致しています。これは、量子重力効果を含めた場合でもマルダセナの仮説が成立することを裏付ける証拠の第一号となりました。実際、Nature.comに掲載されたコラムで、マルダセナ博士が「どうやら彼らの計算結果は正しそうだ」とコメントしています※2。
ゲージ理論の数値計算を可能にした「箱」
コンピュータを使って計算するところに特徴があったこの研究。どのような数値計算をコンピュータにさせればよいかというプログラムはありましたが、結果が出るまでに3～4年の時間を費やしました。
図2のグラフを書くのに必要な数値計算は、合計で半年もの時間がかかりました。それに加えて研究初期の数値計算の方法では、計算を進めていくうちに、対象とする粒子が束縛状態でなくなってしまう不具合が起きたのです。ブラックホールは、狭い領域に閉じ込められているのが特徴です。しかし、構成する粒子がどこかへ飛び出していってしまうとブラックホールが崩壊し、それ以上計算が続けられなくなってしまうのです。
そこで伊敷さんは、計算対象の粒子を「箱」に入れた状態で計算することを思いつきました。といっても普通の箱ではありません。「箱」の壁が粒子を自然界ではありえないほどに跳ね返したり、粒子の束縛を不自然に手伝ったりするようでは、ブラックホールの真の姿を表したことになりません。あくまでも“自然な”壁を持つ「箱」を用意したのです。
「箱」は、束縛状態を長く保つのにとても役立ちました。伊敷さんはさらに、「箱」の大きさで計算結果が影響を受けるかどうかを確かめました。大きさで計算結果が変わらないことを確認できたことで、「箱」の導入が正解だったと結論づけたのです。
普遍性を検証していきたい
今回の研究では「ゲージ理論と超弦理論は等価性を持つ」ことの一例を示すことができました。しかし、伊敷さんは「ゲージ理論と超弦理論は等価性を持つと結論づけるためには、まだまだ多くの研究が必要です」と言います。他のパラメータや他のゲージ理論を用いた計算など多くの事例で対応していることを検証しなければ、「一般的な」理論とすることはできないのです。
伊敷さんは、ゲージ理論の次元を上げていきたいと考えています。今回検証したのは、1次元のゲージ理論と10次元の超弦理論との対応です。もともとマルダセナ博士が提唱したのは、4次元のゲージ理論と10次元の超弦理論との対応でした。伊敷さんは、ゲージ理論の次元を4次元まで上げようと計画しています。4次元の数値解析は1次元とは比べものにならないほど複雑になります。多くの研究者がチームを組み、幾多のコンピュータやスーパーコンピュータを使用し、計算時間を短縮する工夫も必要になってくるでしょう。
これまで、伊敷さんらをはじめとする少数のグループが、この研究領域を切り開いてきました。伊敷さんは「もっと多くの研究グループが参入し、より大きな研究分野に育っていってほしい」と考えています。そうしてこの研究分野が活気づいてくれば、ゲージ理論と超弦理論の対応は普遍だということが明らかになっていくでしょう。
曲がった空間についての研究が進めば、ブラックホールだけでなく、ビッグバンが起こる前の初期宇宙についてのなぞが解ける日もくるかもしれません。
用語解説
- 1 「量子ブラックホールのホログラム的記述の数値的検証」
- M. Hanada, Y. Hyakutake, G. Ishiki and J. Nishimura, “Holographic Description of a Quantum Black Hole on a Computer”, Science Online, Apr 17, 2014
http://www.sciencemag.org/content/344/6186/882.full - 2 超弦理論でなくてもブラックホールを理解できるのではないかという画期的な考えを1997年にアルゼンチン出身のマルダセナ博士が発表しました
- マルダセナ博士のコメント“It seems to be a correct computation”。Nature.com
http://www.nature.com/news/simulations-back-up-theory-that-universe-is-a-hologram-1.14328 - 3 温度とブラックホール質量の関係
- 物理学者ホーキングは、1974年にホーキング輻射という仮説を発表した。ブラックホールがあたかも温度をもった物体として振る舞い、粒子を放出して次第に蒸発していくという考えである。ブラックホールの周囲では、エネルギーを持った真空から粒子と反粒子が対生成している。生成した粒子と反粒子がぶつかると対消滅が起こるが、まれに反粒子がブラックホールに吸い込まれ、粒子がブラックホールの外に放出されることがある。
伊敷さんらは本研究において、温度と内部エネルギーの関係を調べた。内部エネルギーはADM質量と呼ばれ、これはブラックホールに対して定義される質量と等価の指標である。つまり、温度によって質量がどう変化するかというブラックホールの熱力学的な性質を調べることにつながる。
