アインシュタインが出した宿題を解く －ブラックホール研究の先にある物理

光さえも吸い込んでしまうため真っ暗に見えるブラックホール。「吸い込むだけでなく、ブラックホール誕生初期には、とてつもないものを出しているんです」と京都大学の関口 雄一郎（せきぐち・ゆういちろう）特任助教は言います。ブラックホールができる過程をシミュレーションしている関口さんがその研究の先に見据えているのは、「およそ100年前にアインシュタインが出した宿題」とのこと。時空を超えた物理研究のお話を伺いました。

ブラックホールを作る

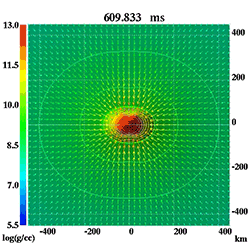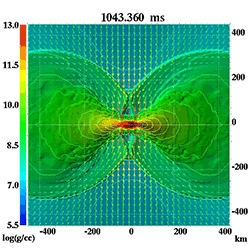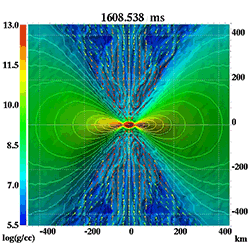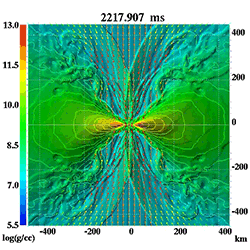
関口さんは「私はブラックホールを作っています」と自身の研究を紹介します。いったい、どうやったらブラックホールを作ることができるのでしょうか。まずは、関口さんが2011年に作ったブラックホールをご覧ください。

動画は恒星が終末期に超新星爆発を起こし、その後、ブラックホールができる様子をシミュレーションしたものです。星の内部で対流が起こったり、降着円盤と呼ばれるディスク状の構造ができたり、星の表面からジェット状に物質が放出されるアウトフローが発生したりと、複雑な現象が連続して起こっているのがわかります。

2005年に関口さんがシミュレーションしたときには、これほど複雑な現象を示すブラックホールを作れず、ただ、星がつぶれて収縮するという計算結果でした。6年の研究の積み重ねで、ブラックホールを追跡するための数値的技法を開発できたことに加え、微視的物理と呼ばれる複雑な過程を盛り込み、それを取り扱う数学的手法も発展してきたので、冒頭の動画のように複雑な現象を追えるようになりました。

宇宙空間で、物質に働く力は4種類。関口さんの研究では4つすべてを考慮にいれています。極限状態の超高密度物質に働く核力などの「強い力」、ニュートリノと物質の相互作用などを記述する「弱い力」、電磁気力、重力をすべて考慮にいれた複雑な計算をしているのです。きちんと計算しようと思うと、4種のうちの一種類だけでもスーパーコンピュータが必要なほどの複雑さです。関口さんの計算プログラムではいくつかの簡略化を行っていますが、それでもその長さは10万行を軽く超えるそうです。

ブラックホール研究の先にみすえている基礎物理

関口さんは「ブラックホールのシミュレーションは、アインシュタインが出した宿題を解くヒントを出せるはずだ」と考えています。

アインシュタインは、一般相対性理論のなかで重力波の存在を予言しました。しかし、まだ重力波を直接とらえてはいません。もし、この重力波を観測、実証できたらノーベル賞は間違いないといわれています。

現在、この重力波を捕らえるための実験装置KAGRA（かぐら）を岐阜県の神岡鉱山に建設中です。重力波は、たとえば連星中性子星が合体してブラックホールができるときに放出されます。しかし、重力波を観測するには、地球と太陽の距離がわずか原子1個分だけ変動するような、極微の空間のゆがみを検出しなくてはなりません。このようにわずかなゆがみをとらえるには、やってくると期待される重力波に関する予言を行い、その予言と実際のデータの整合性を確かめる形で観測しなければなりません。観測に際して、理論側が提供する狙いどころが重要となるのです。「この時間に連星中性子星が合体しました。そうすると、この方向から、このような波形の波が来ているはずなのです」という狙いどころをシミュレーション結果から出せるのです。

重力波という新しい観測手段によって、宇宙に関する理解は大きく進展すると期待されます。このようにブラックホール研究の先には、先人が発展させてきた基礎物理の真理をさらに追究するという壮大な夢が広がっているのです。

ブラックホール研究の難しさ

関口さんは、「ブラックホールを扱う一般相対性理論のシミュレーションはとにかく複雑で大変なんです」と言います。

あまりにも複雑な物理を扱うため、シンプルな微分方程式では現象を表現できないところもあるのです。たとえば「強い力」は、実際にシミュレーション中に計算するにはあまりに複雑なため、結果をあらかじめ「表」にまとめておきます。その上で、計算の途中でコンピュータにこの「表」を参照してもらい、「シミュレーションで得られた、こういう密度でこういうエネルギーでこういう熱力学状態を一番再現するのは「表」の中でどの状態にあたるのか」という探索を行い、その探索結果を反映して次の計算へ進むという過程もあります。

アインシュタイン方程式を解くにも注意が必要です。この方程式はエネルギーと運動量がきちんと保存されるように解かないと、計算が破綻してしまうことが知られています。ですから、エネルギーと運動量が保存するように計算式を立てるというしばりのなかで計算を進めます。

また、ニュートン力学では、質量は重さと単純に考えることができます。しかし、相対性理論では「速く動くと重くなる」のです。ですから、質量を考えるときには、そこに「速さ」の情報も必要になります。そして、温度が高いことは相対論的には重いことを指します。結局、質量を考えるときには、速度と温度の情報も計算しなければなりません。

さらに難題が続きます。先ほど述べた「表」を探索するには、密度の情報が必要です。密度を求めるときには速度と温度による効果を補正する必要がありますが、この温度は「表」を用いて初めて求まります。「表」を用いるためには密度の情報が必要ですが、その密度はいま求めようとしていたものです。つまり、「密度」が循環してしまうのです。解析的に書き下された方程式になっていれば、式を解けば答えは出てきますが、計算の途中には「表を参照」というステップが入ります。結局、非常に手間のかかる計算をしなければならないのです。

そして、関口さんの研究ではニュートリノが非常に重要になります。ニュートリノは「弱い力」で記述されます。「弱い力」といっても、「重力」よりは十分に強い相互作用です。

シミュレーション中に強さが大きく異なる複数の相互作用が入ってくる場合には注意が必要です。ブラックホール形成を追跡するためには、「重力」で特徴づけられる「長い」時間のシミュレーションを継続する必要がありますから、時間経過の最小単位はそれに応じて長く設定されます。しかし、重力よりはるかに強い「弱い力」による相互作用は、「長い」時間経過では追跡することができません。そのため、単純な計算法では正しい結果が得られなかったり、計算中に「弱い力」による相互作用の部分が暴走的に大きくなったりして、計算自体が破綻してしまうこともあります。これらを避けるため、一般的に「陰的スキーム」と呼ばれる手法を用いますが、すでに述べた相対性理論特有の難しさのため一筋縄ではいかず、ここでも計算は複雑にならざるを得ないのです。

スーパーコンピュータへの期待

スーパーコンピュータ「京」は「（世界）最速」と表現されますが、関口さんは、「計算速度にもいろいろあるんです」と言います。

関口さんが求める「速い」コンピュータは、シンプルな計算をひたすら速く計算するタイプではなく、複雑な計算でも速く行うことができるもの。そのためには、計算機が条件分岐などの複雑なプログラム構造に対して強く、コンピュータ内部の「通信速度」が速い必要があるのだそうです。

京のようなコンピュータがあるからこそ、関口さんは複雑な計算式を用いて研究できるようになってきました。しかし、「京の計算能力の10%は必ず引き出してほしい」という使用条件は、関口さんの研究にとってはハードルが高いといいます。

計算能力を引き出すには、計算式を京が使いやすいように「チューニング」する必要があります。このチューニングは物理とは違ったコンピュータの知識が必要で、使用するスーパーコンピュータの個性をしっかりと理解したうえで、オーダーメイドのチューニングを行う必要があります。「今後、スーパーコンピュータの性能がもっと上がっても、チューニングの専門家や利用者への支援体制がもっと拡充されていかないと、せっかくのコンピュータを十分に使いこなせない事態を招くのではないか」と関口さんは心配顔です。

そんな関口さんが研究の喜びを感じるのは、「計算のバグをみつけられたとき」とのこと。軽く10万行を超える計算コードのなかから不具合をおこしている箇所をみつけるのは至難の業。この分野で世界をリードする関口さんですが、「自分とはまったく異なる発想をしてくれる仲間がほしい」と思いながら研究をしているそうです。