原子核の正体を解き明かす | 計算基礎科学連携拠点

物理学の教科書にあった「原子核の形は楕円になる」という何気ない記述を学部生時代に見た、東京大学大学院理学系研究科特任助教の吉田亨（よしだ・とおる）さんは、「本当だろうか。どんな計算をしたら楕円だとわかるのかな」と疑問を抱いたそうです。それが、原子核研究の世界へと進むきっかけとなりました。
吉田さんの研究テーマは、原子核の様子を方程式で記述するのに必要な物理量を明らかにし、原子核を表す最適な理論を見出すこと。その進展はというと「うまく行き過ぎていて、“本当かな”と慎重になっているところです」。吉田さんの気持ちを高ぶらせる最近の研究成果についてうかがいました。

原子核の基本となる殻模型

図1　殻模型。原子核の中心に陽子と中性子の塊（ピンク部分）があると仮定し、その周りを陽子（オレンジの球）や中性子（緑の球）といった核子がグルグルと運動しているモデル。原子核内を陽子や中性子が比較的自由に運動できることから、全体を液滴と近似することができる。

原子核を構成する陽子と中性子の振る舞いを研究する場合、メイヤー・イェンゼンによる「殻模型（シェルモデル）」が基本の形と考えられてきました（図1）。殻模型とは、原子核の中心には塊があり、その周りを陽子や中性子がグルグルとまわっている、とするモデルです。宇宙になぜヘリウムや酸素、鉄が多く存在しているのかが示せる、大変説得力のあるモデルでした。

従来の殻模型は、エネルギーレベルが低く安定な状態や、丸い原子核の状態を表すのに都合が良いモデルです。ところが、宇宙にはさまざまな形をし、またエネルギーレベルも高い状態が存在しています。原子核を正確に表すためには、エネルギーレベルが低い状態だけでなく、高い状態をも表すモデルを考えなければなりません。

アルファクラスターモデルを用いた原子核の解析

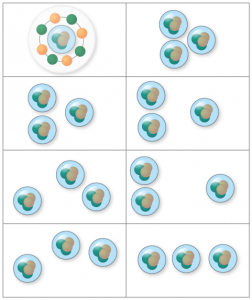
図2　炭素12原子核のアルファクラスターモデル。陽子2つと中性子2つからなるアルファ粒子（ヘリウム原子核）3つで炭素12の原子核が構成される。左上は殻模型と同じ状態。アルファ粒子3つが同じ場所で重なり合った特殊な形と考えられる。アルファクラスターモデルはシェルモデルにくらべると広がっており、密度が低い。殻模型が液滴に近似されるのに対して、アルファクラスターモデルは気体に近似できる。

エネルギーレベルが高い原子核を考えるとき、「アルファクラスターモデル」を用いると多くの現象や実験結果を矛盾なく説明できる、という経験則があります。アルファクラスターモデルでは、陽子2個と中性子2個からなるヘリウム原子核（アルファ粒子）がぶどうの房（クラスター）のように集まって原子核を作っていると考えます。このモデルによれば、ベリリウム原子核（陽子4個、中性子4個）はアルファ粒子2つから構成され、炭素原子核（陽子6個、中性子6個）はアルファ粒子3つからなると考えられます（図2）。

吉田さんは1年前までは、このアルファクラスターモデルを用いて研究していました。吉田さんの一日は、朝一番にスーパーコンピュータを操作するターミナルやグラフィカルソフトを立ち上げるところから始まります。原子核が持つエネルギーはどのような計算式で記述できるのかを理論立てて考え、計算を始めます。このような計算は莫大な量なので、スーパーコンピュータを使っても一日がかりの計算になることもあります。理論計算の結果から導き出されたエネルギーレベルの値が実験値^※1とどの程度一致しているのかを確かめます。一致していれば、その日作成した計算式は「確からしい」ということになります。

吉田さんの研究成果、炭素12（陽子6個、中性子6個）の原子核について紹介します。図3上の実験と理論（吉田さんの計算結果）のグラフを比較すると、原子核のエネルギーレベルの高いところから低いところまで、よく一致しています。この理論は、アルファ粒子3個が近づいている状態だけでなく、距離的に離れた状態も考慮に入れた場合です（図3下）。アルファ粒子3個の距離をさまざまに仮定し、すべて考慮に入れることを、状態の「重ね合わせ」と言います。

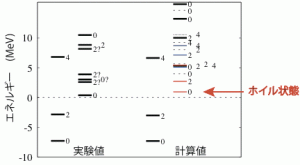
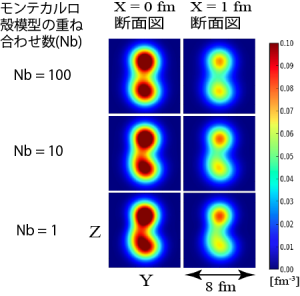
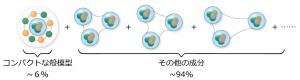図3　アルファクラスターモデルによる炭素12原子核のクラスター構造の分析。アルファ粒子3つの距離が近づいた状態から離れた状態まで、さまざまな状態の重ね合わせで原子核のエネルギーを計算した（右側）。実験から得られたエネルギースペクトル（左側）とよく一致している。またホイル状態として知られている状態については、殻模型状態は6％程度の寄与と、距離的な広がりをもったその他の成分が94％程度寄与していることが分析できた。

この研究で吉田さんは、他の研究者が4～5種類の振動を重ね合わせていたのに対して、100にのぼる振動を重ね合わせて計算しました。エネルギーレベルの違いを一つひとつの特徴に特化しているような数学的な処理でなく、エネルギーレベルの違いのお互いの関係性をSU(3)やSp(2)代数という数学的手法を使って計算するように工夫したことが成功の秘訣でした。

吉田さんは、アルファクラスターモデルの欠点の一つは「パラメータが多い」ことだと言います。ある程度の根拠を持って設定する現象論的パラメータではあるのですが、エネルギーレベルがよく一致するようにパラメータによる合わせ込みをしている感も否めないとのこと。
原子核と核子をつなぐ途中にクラスターという階層を用意し、そこでおおよそを議論するというイメージです。この方法はうまくいくことも多いのですが、計算結果が一致していても、原子核全体を核子から理解したとはなかなか言えないのだそうです。

モンテカルロ殻模型を用いた原子核の解析－第一原理計算を元に

原子核全体を理解するためには、陽子一つひとつ、中性子一つひとつの振る舞いを数学的に記述する「第一原理計算」に基づく研究をすべき。これが多くの物理学者の目標です。核子がもともと持っている性質を計算に反映させる方法で、パラメータによる合わせ込みをしないで良い手法なので、より説得力のある理論を導き出せると考えられるからです。ところが、それは非常に複雑な計算と膨大な計算時間が必要になってしまい、これまでは困難でした。ところがモンテカルロ殻模型と呼ばれる新たな手法が発達してきたことによりこの壁が打ち破られ始めています。

この状況の中で、吉田さんは密度分布などの基本的な量を計算するときに、多数の「重ね合わせ」でも数学的にうまく処理できる方法を見出しました。これなら、第一原理計算に基づく研究とクラスター構造の研究がつなげられるのではないかと吉田さんは考えました。

図4　ベリリウム8の陽子の密度分布図。重ね合わせの次元が低くても高くてもアルファクラスター構造が安定して現れている。

吉田さんは、第一段階として計算が行えそうな陽子4つと中性子4つのベリリウム原子核について、第一原理計算に基づくモンテカルロ殻模型を用いた計算を行いました。原子核の形がどうなっているかを確認すると、みごとにクラスター構造を示していました（図4）。これが、「うまく行き過ぎて本当かな」と吉田さんを慎重にさせる研究結果です。

これは、アルファクラスターモデルでは「仮定」あるいは「前提」としていたアルファクラスター構造が、第一原理計算に基づく計算で検証されうることを示しています。

吉田さんは、ベリリウム8などの軽い核のより詳しい性質を調べ終えたら、もっと重い原子核や、もっとエネルギーレベルの高い状態まで考慮に入れた計算をすることに挑戦したいと言います。そのためにはスーパーコンピュータ「京（けい）」のような大規模計算機が必要です。これらの計算で、吉田さんの見出した計算式がどの程度、多くの現象を説明できる磐石な理論なのかを慎重に確かめ、発展させていきたいと考えています。