万物に質量を与えるメカニズムに欠かせないとして、その発見の期待が高まるヒッグス粒子。でも、今回ご紹介する高エネルギー加速器研究機構(KEK)特任助教の伊藤 悦子(いとう・えつこ)さんは、「ヒッグスという素粒子は存在しないのかもしれません」と言います。これは衝撃的です。
ヒッグス粒子は、ビックバンで生まれた宇宙が冷え、エネルギーが下がる過程で素粒子に質量が与えられるメカニズム構築のために考え出された理論上の素粒子です。欧州合同原子核研究機関(CERN)がスイス・ジュネーブ郊外で行っているLHC実験でこれを見つけようとしていることが何かと話題になっているので、耳にしたことのある方も多いはず。
素粒子標準模型とヒッグス粒子
素粒子は、物質を究極的に細かくしていってたどりつく、最も基本的な構成要素です。原子の中心には原子核があります。最も小さい水素原子核でおよそ1兆分の1ミリメートルという極めて小さいスケールです。ところがこれで終わりではなく、さらに小さな構造があるのです。
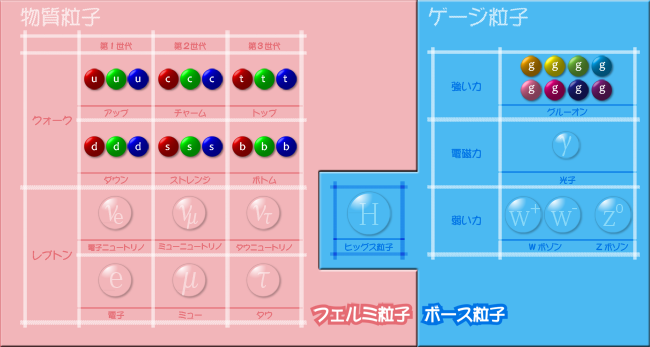
図1 素粒子標準模型。背景ピンクがフェルミ粒子、水色がボース粒子。
原子核はクォークやグルーオンといった素粒子が、ある法則のもとで結合していることがわかっています。そんな途方もなくミクロな世界は肉眼ではおろか、顕微鏡でさえ見ることはできません。ではなぜ「わかっている」と言えるのでしょうか? 研究者は、目には見えなくとも、あらゆる実験データから読み取れる素粒子のふるまいを統一的に説明できる理論体系を作ることで、素粒子の世界を理解しようとしているのです。理論体系は「模型」と呼ぶこともあります。クォークと、電子・ニュートリノの仲間であるレプトンを分類し、それらの相互作用のメカニズムを解き明かした集積が「素粒子標準模型」としてまとめられています。(図1)

図2 π+中間子。フェルミ粒子(uクォーク)と反フェルミ粒子(反dクォーク)の複合状態。
図1を見ると、クォークや電子、ニュートリノといった物質粒子はフェルミ粒子、ヒッグス粒子はボース粒子であることがわかります。ボース粒子はいくつでも同じ状態で同じ場所に入ることができますが、フェルミ粒子は、自分の縄張りに他の粒子を入れてくれません。複数のフェルミ粒子によって作られる複合粒子はつぶれることがなく、物質の材料となれます。
フェルミ粒子と、その反物質である反フェルミ粒子が結合すると、一見、ボース粒子のようにふるまうことができます。たとえば中間子はクォークと反クォークの複合状態で、原子核を結び付けるボース粒子としてふるまいます(図2)。逆にボース粒子からフェルミ粒子をつくることはできません。その意味でフェルミ粒子の方がより根源的な存在であるといえます。
テクニカラー
「ヒッグス粒子も、より根源的なフェルミ粒子が結合してできていたら、美しいと思います。私は、ヒッグス粒子は中間子のような複合粒子で、テクニクォークと呼ばれるフェルミ粒子でできているのではないかと考えています」。伊藤さんはそう話します。
このような理論を「複合模型(テクニカラー)」と呼んでいます。これは1979年にSusskindによって提唱された理論で、名前はクォーク・グルーオンの理論である量子色力学(QCD)からのもじりだといわれています。さらに、このアイデアが実験結果と矛盾しないように拡張したウォーキング・テクニカラーという模型が、1985年頃にHoldomやMiransky、名古屋大学の山脇幸一教授によって提唱されました。このテクニカラー理論は、QCDより1000倍ほども高いエネルギー領域で現れる理論です。スケールは1/1000になって、さらに極微の世界に入り込むことになります。
QCDでは、クォークと反クォークが強い力で凝縮することで質量が生み出されると考えられています。実際、KEKの研究グループが数値シミュレーションによってこれを確かめました。さらにミクロな世界で全く同様なことが起こっていて、そこで生じた凝縮こそがヒッグス粒子の正体なのだというのがテクニカラーのアイデアのポイントです。スケールは違えど、同じことが起こっているというのはなかなか魅力的な考え方です。
でも、これが現実的な理論といえるためには、対称性や実験結果との整合性など、クリアしなくてはならない条件がいくつもあります。理論の性質を調べて、実現の可能性を確認するためにうってつけなのが、格子場理論の数値シミュレーションです。時空を格子状に区切って数値計算する格子QCDと同じ手法です。
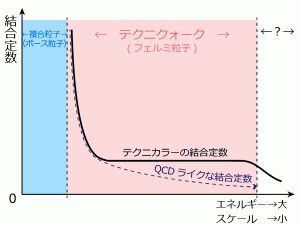
図3はクリアしなくてはならない条件を満たす場合に、テクニクォークとテクニグルーオン(テクニクォークと相互作用するゲージ粒子)との間に働く力の強さを表す「結合定数」のグラフです。結合「定数」と呼ばれてはいますが、エネルギーによって変動する値で、どのように変動するかは理論によって決まります。縦軸は結合定数の強さ、横軸はエネルギーです。素粒子を扱う場合、エネルギーが高い=距離(スケール)が短い、ことになります。
「図3には、結合定数がエネルギーによらず成長しなくなる領域がありますよね。これが面白いと思うんです」伊藤さんは目を輝かせます。「エネルギーによらないということは、温度にもよらないということです。それって不思議だと思いませんか?」そのような世界では、生卵を鍋で何時間ゆでても、冷凍庫で何時間凍らせようとしても、生卵のままです。確かに不思議です。でも本当にそのような不思議な理論は成り立つのでしょうか?
テクニカラーが実現するためには、その理論に登場するテクニクォークとテクニグルーオンとの結合が特殊な振舞いをする必要があります。図3に示したように、高エネルギー領域では小さく、ある境目より低エネルギーの領域では極めて大きく、その中間領域ではほとんど変化しないようになっていなければなりません。一方でこの理論では、テクニクォークやテクニグルーオンの種類や数が、今のところわかっていません。
標準模型では、クォークがアップ(u)、ダウン(d)、ストレンジ(s)、チャーム(c)、ボトム(b)、トップ(t)の6種類あることがわかっています。これに相当する情報を図3のような結合定数の振舞いを実現しつつ探ることが、世界的に盛んに行われています。伊藤さんたちの研究グループでも着々と成果を上げつつあるところです。
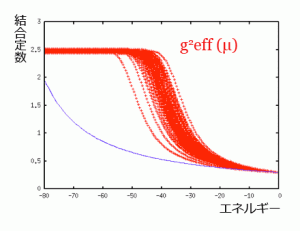
図4に、伊藤さんと大阪大学などのグループによる成果を示します。確かに結合定数が成長しなくなる領域があります。ある境目より低エネルギーの領域で、結合定数が極めて大きくなるような理論は、比較的容易に組み立てることができます。ということは、本当にヒッグス粒子は素粒子ではなく、テクニクォークが結合した複合粒子なのでしょうか?
「それはまだわかりません。実はテクニカラー以外にも余剰次元模型や超対称な模型などの理論が世界中で盛んに研究されています。ヒッグス粒子、あるいはまた別のメカニズムかもしれませんが、そのあたりのより確かな情報は今後、LHCの実験で明らかにされるでしょう。どのような結果が出るか楽しみです」。
理論図を描く
小さいころから考えることが好きだったという伊藤さん。「趣味は囲碁です。囲碁にはきっと必勝法があると思うんですよ。それを追い求めるのがおもしろいんです」。囲碁と素粒子理論に共通点があるとしたら、「囲碁も理論もルールは単純なのに、奥深いところが似ています。どちらも完ぺきに理解したいです」と言います。理論を完璧に理解するにはどうすればよいのでしょうか? 「たとえば、理論図を埋め尽くすことができれば、その理論について完璧に理解できたことになるのではないでしょうか」。
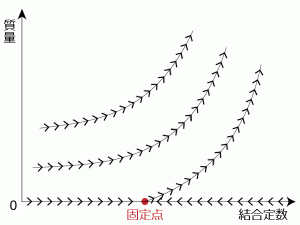
図5に理論図を示します。結合定数はエネルギーに依存する値で、どのように依存するかは理論によります。逆に、質量、結合定数といった理論を決定づける値をプロットすると、その理論の全体像を知ることができます。図4で見たように、結合定数がエネルギーによらない点をその理論の固定点(図5の赤丸)といいます。
理論図を見ると、理論に流れがあり、固定点に理論が集約したり、固定点から理論が出て行ったりしています。伊藤さんはテクニカラーの候補となる理論の固定点を2011年に探し当てました。固定点上の理論は「共形場の理論」とよばれ、厳密に物理量を計算できる、つまり理論が解けることがあります。この共形場の理論の性質を調べることが、伊藤さんの研究テーマの1つです。「これからも、いろんな理論の理論図を描いていきたいです」。