物質を、分子、原子、原子核と小さな単位に切り分けていくと、物質の最小構成要素である素粒子にたどり着きます。「地上で起こる現象をとてもよく説明できる素粒子の理論（標準理論）はあるのですが、宇宙を見上げるとこの理論では説明できない現象があり、謎が残されています」と言うのは高エネルギー加速器研究機構の金児隆志（かねこ・たかし） 研究機関講師。高精度の格子QCDシミュレーションで、まだ解明されていない「新物理」の謎に迫ろうと、スーパーコンピュータ「富岳」を使って大規模計算に取り組んでいます。
新物理発見の鍵を握る「B中間子の崩壊」
ノーベル物理学賞を受賞した小林・益川理論の発表は1973年のこと。当時、素粒子の一種であるクォークは３つのフレーバーしか発見されていませんでした（フレーバーとは、クォークや別の素粒子であるレプトンの種類のことです）。そんなときに二人が「６フレーバー以上のクォークが存在する」と予言したのは非常に先駆的でした。この理論はクォークのフレーバーが「ダウン、ストレンジ、ボトム」から「アップ、チャーム、トップ」のいずれかへ、あるいはその逆へと変化する素過程（相互作用）を導入し、「小林・益川行列要素」が各過程の起こりやすさを表します。
\(q\)（あるフレーバーのクォーク）が弱い相互作用を媒介する素粒子Wボソンを放出しながら \(q′\)（別のフレーバーのクォーク）に変化する。ダウン（\(d\)）、ストレンジ（\(s\)）、ボトム（\(b\)）の３フレーバーのクォークからアップ（\(u\)）、チャーム（\(c\)）、トップ（\(t\)）の３フレーバーのクォークへの変化の起こりやすさを３×３の行列\(V_{qq’}\)(小林・益川行列要素、図中青字)で表す。写真は小林誠博士（左）と益川敏英博士（2001年9月26日撮影、提供：KEK）。
このクォークのフレーバー変化は、加速器を使った実験で観測できます。クォークの変化の中で、特に新物理の謎を解く鍵を握ると考えられ、世界中で研究が進められているのがB中間子の崩壊です。B中間子は重いボトムクォークと軽いクォーク（アップまたはダウン）からなる複合粒子(ハドロン)です。
図2：茨城県つくば市にあるBelle II測定器
2019年に本格的な実験が始まり、2030年初頭までに精密な測定が行われる予定（写真はウィキペディアより）。
しかし、「新物理を発見するためには理論の精度も上げる必要があります。精密実験測定の結果と、精密な理論予言（精密標準理論計算）とを比較して初めて、新物理のヒントが見つかってくるのです」と金児さん。精密な実験データを最大限に生かすためには、それに見合う精度の理論計算が必要となるのです。
そこで金児さんは、スーパーコンピュータ「富岳」を使って、精密標準理論計算に取り組んでいます。その中でも、精密な理論計算に大きく寄与する「強い力の効果」を格子QCD（Quantum Chromodynamics：量子色力学）の計算機シミュレーションで求める研究を進めています。現在、金児さんが研究対象にしているのは、セミレプトニック崩壊（図3）。Belle II実験で精度が格段に上がると期待されている崩壊です。
図3：セミレプトニック崩壊
多様な粒子の崩壊パターンのうち、ハドロンとレプトンが生じる場合をセミレプトニック崩壊と呼ぶ。中でも、金児さんの研究対象はB中間子がπ中間子（ハドロンの一種、アップまたはダウンクォークとその反クォークからなる）とレプトン（\(\ell\)、電子または\(\mu\)粒子）になる崩壊。ニュートリノ（\(\nu\)）も放出される。この崩壊振幅（絶対値の２乗が崩壊確率を与える）は、図の右辺で表される。このうち、“電磁気力＋弱い力の効果“は電弱統一理論で解析的に手計算できる。強い力の効果をQCDシミュレーションで求めて実験結果と比較すると、”小林・益川行列要素“が決まる。次に、その”小林・益川行列要素“を使った計算結果と、別のセミレプトニック崩壊の実験結果を比較すると、新物理のヒントが得られる。
実験に見合う高精度の格子QCDシミュレーションを
金児さんが研究するQCDはクォーク間に働く強い力を説明する理論です。これを時空格子上に定式化したものが格子QCDです。この理論は、QCDの数学的に厳密な定義を与えるだけでなく、計算機シミュレーションの基礎を与えます。格子が交わる点にクォークや反クォークを、辺に強い力を媒介するグルーオンを配置し、格子の交点と辺のみにクォークやグルーオンを存在させると理論の自由度が有限となり、計算機のメモリ上にその世界を再現することができるのです。
図4：格子QCD計算
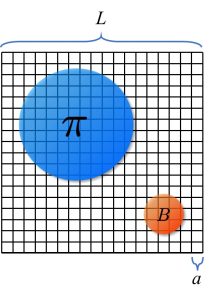
格子サイズ \(L\) を大きく、格子間隔 \(a\) を小さくすると精密な計算に近づく。実際の計算は４次元の格子を考慮して行うが、ここでは、見やすいように２次元で示している。
さらに、金児さんが精密化のためにこだわった点がもう一つあります。それは、クォークのフレーバー間の「カイラル対称性」を保つということです。例えば、陽子は3個の軽いクォークからなっていますが、各クォークの質量を合わせたよりもはるかに大きい質量をもっています。これは、感覚的には理解しがたい現象ですが、カイラル対称性が自発的に破れてクォークが大きな有効質量を獲得するためだと説明できます。このように、カイラル対称性はクォークの性質に深く関わるものであり、格子QCD計算においてカイラル対称性を保つと、格子を使うことによる誤差を大きく削減できることがわかっています。
しかし、カイラル対称性を考慮するシミュレーションは非常に複雑なため、従来の研究では、カイラル対称性を壊して計算量を減らすというのが定石でした。金児さんと共同研究者は「『富岳』の計算能力を使えば、カイラル対称性を保った精密シミュレーションができるはず」と考えました。そして、カイラル対称性を保ちつつも、計算コストを減らす工夫を盛り込んだシミュレーションの方法を開発しました。さらに、「富岳」の特長を生かした高速なシミュレーションが行えるように、プログラムのチューニングを行いました。これにより、より実際の状況に近い高精度なシミュレーションが可能になりました。
金児さんは、2014年度から2019年度にかけて行われたポスト「京」重点課題⑨で計算プログラムを開発し、計算精度10%を達成していました。そして、2020年からは「富岳」成果創出加速プログラムで上の研究を進めています。目標精度は、ここ数年でBelle II実験が到達する予想精度「５％」です。
2022年12月現在、シミュレーションの精度は図5のように上がってきています。金児さんは「カイラル対称性を保つ理想的な定式化と高性能なスーパーコンピュータ『富岳』を用いて誤差を制御したからこその成果です。おそらく、成果創出加速プログラムが終了する2022年度末には、目標精度の５％を達成できるでしょう」と自信をのぞかせます。
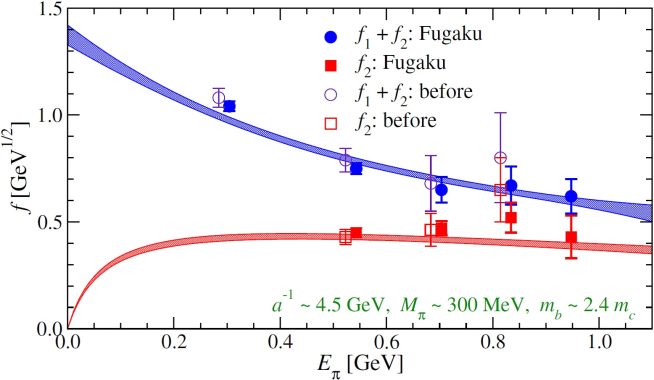
図5：「富岳」でシミュレーションした形状因子
QCDの効果を記述する形状因子をシミュレーションで計算した。２種類の形状因子 \(f_1+f_2\) と \(f_2\) をプロットしている（塗りつぶしたシンボル）。ポスト「京」重点課題で計算していたとき（白抜きのシンボル）よりも誤差（各点から上下に伸びる誤差バーの幅）が小さくなっている。赤と青の帯は理論的に期待される関数形に当てはめたもので、小林・益川行列要素|\(V_{ub}\)|の決定に必要となる。「富岳」では高エネルギーの点も計算したので関数の信頼性が上がっている。横軸はπ中間子のエネルギー、縦軸は、形状因子の値。
さらなる高みを目指して
Belle II実験は2030年代初頭まで実験データを蓄積して誤差を減らし、測定の精度を上げていく予定です。金児さんは、「そのときの最終精度に見合うだけの理論精度を出すために、今ある研究の延長ではなく、さらなる高精度化が必要です」と言います。現在は、アップ・ダウンクォークを重く、ボトムクォークを軽くするという近似をして、格子のサイズが非常に大きくなったり格子間隔が非常に細かくなったりするのを防いでいますが、さらに精度を上げるためには、この近似を取り払わなくてはなりません。「そのためには、『富岳』よりも計算性能の優れたスーパーコンピュータが必要になります」と金児さん。
一方で、金児さんらが開発したカイラル対称性を保った計算手法は今回研究対象に選んだセミレプトニック崩壊以外のクォークの変化にも応用可能です。たとえば、レプトンのみを生成するレプトニック崩壊、ハドロンのみを生成するハドロニック崩壊、中性B中間子とその反粒子の混合など数多くの反応に使えるのです。幅広い研究対象にこの計算手法が使われれば、まだ誰も見つけていない新物理のヒントが見つかっていくかもしれません。金児さんはさらなる高みを目指して研究を続けています。
