原子の構造は「陽子と中性子からなる原子核の周りを電子がまわっている」と中学で習います。しかし、「原子核の構造にはわからないことがまだまだ残されています」と東京大学理学系研究科 附属原子核科学研究センター特任准教授の清水則孝さんは言います。清水さんはスーパーコンピュータを使って原子核の状態をシミュレーションする理論物理の研究をしています。その研究の魅力を清水さんは「理論研究者が新しい発見をすると、それが実験研究者の新たな発見の役に立つ。実験研究が進展すると理論研究も進展していく。そうして次々にわからなかったことがわかってくるところが面白い」と言います。清水さんが明らかにした原子核研究の成果をご紹介しましょう。
原子の構造は「陽子と中性子からなる原子核の周りを電子がまわっている」と中学で習います。しかし、「原子核の構造にはわからないことがまだまだ残されています」と東京大学理学系研究科 附属原子核科学研究センター特任准教授の清水則孝さんは言います。清水さんはスーパーコンピュータを使って原子核の状態をシミュレーションする理論物理の研究をしています。その研究の魅力を清水さんは「理論研究者が新しい発見をすると、それが実験研究者の新たな発見の役に立つ。実験研究が進展すると理論研究も進展していく。そうして次々にわからなかったことがわかってくるところが面白い」と言います。清水さんが明らかにした原子核研究の成果をご紹介しましょう。
原子核をなぜ理解したいのか
そもそも、原子核の理解を進める研究にはどのような意義があるのでしょうか。研究が進むと、陽子や中性子の数を増減するための核変換技術に必要な基礎物理量がわかってきます。もし、陽子や中性子の数をコントロールできる核変換反応が可能になれば、原子力工学への応用ができます。放射性廃棄物を効率よく減らせるような手法の開発にも役立つはずです。
基礎物理量の理解は、宇宙でどのように物質が作られていったのかという創生史の理解にもつながります。清水さんは、「ニュートリノはマヨラナ粒子なのか?」という宇宙の起源を知る研究にも自身の研究を応用しています。
世界初の計算を可能にしたKSHELLコードの開発
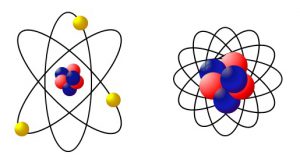
図1:原子の構造(左)と原子核の構造(右)
陽子(青)と中性子(赤)も電子(黄)のように軌道上を運動している。核子(陽子と中性子)の数が2、8、20・・・だとエネルギー的に安定する。2、8、20…を魔法数(マジックナンバー)という。
原子は原子核のまわりにある軌道を電子がまわっており、電子数が2、8、20・・・だと安定します。清水さんは「原子核にも似たような状態が存在します。原子核に相当する中心核がないといった細かな違いはありますが、原子核の核子(陽子と中性子)も軌道上を運動しており、核子の数が2、8、20・・・だと安定な閉殻構造をとるのです」と説明します(図1)。
原子核の状態を知るために清水さんが使うモデルは殻模型*1(図2)です。安定な閉殻の部分はパッケージとして扱い、計算を簡略化できるモデルです。閉殻に入りきらない核子のみ、詳細に計算します。閉殻部の計算を減らせるため、ある程度、核子数の大きい原子核まで計算できるという特長があります。
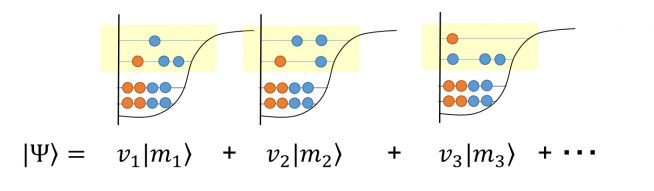
図2:殻模型の波動
黄色で網掛けした核子(●(青)3個、●(赤)1個)のみ計算する。下2段に示した8個の核子(●(青)4個、●(赤)4個)は閉殻として扱う。この図の場合、核子が取りうる軌道(2種類)に3個の核子が入る様子を表している。考え得るすべての状態が重ね合わさっているとして計算をする。
計算に使うモデルは核子数によって適したモデルが異なります。現状の計算環境では、核子数が 16~130あたりの中間質量数の原子核を計算するのに、殻模型の手法が適しています。それより小さい原子核は第一原理計算*2、大きい原子核は密度汎関数法が用いられます。
清水さんは原子核を知るためにシュレディンガーの波動方程式を解きます。波動方程式に含まれる行列の次元数は、たとえば、核子数が56のニッケル56の場合、閉殻部の計算を簡略化しても10億次元になります。10億次元x10億次元の行列に関する方程式をランチョス法と呼ばれる方法で解くことになります。計算量を減らすために、あまりにも不自然な配位はないものと除外して次元を減らすような近似がしばしばおこなわれますが、この近似が結果に悪影響を及ぼすことも多くあります。ですから、近似なしに解くに越したことはありません。これほど膨大な計算の正確性を失わずに、しかも速く計算する工夫に多くの研究者が挑んでいます。
清水さんはKSHELLという新たな計算コードを開発しました。この計算方法は、閉殻部分の核子は計算を単純化していますが、閉殻以外の核子については計算を簡略化せずに計算することができます。KSHELLコードでは最新のスーパーコンピュータを用いて、莫大な数の組み合わせ配位を考慮にいれた計算を高速に実行することができるようになりました。たとえば、10億次元の56Niの原子核の基底状態エネルギー計算の場合、パソコンで数日かかっていた計算が、わずか145秒でできるようになりました。
「KSHELLコード開発では、スーパーコンピュータ『京』の性能をいかに引き出すかという点で苦労しました。どのように計算を分割して多数のCPUに同時にバランスよく計算させるかの戦略を練るのは難しく、工夫を重ねてきました」と清水さんは振り返ります。
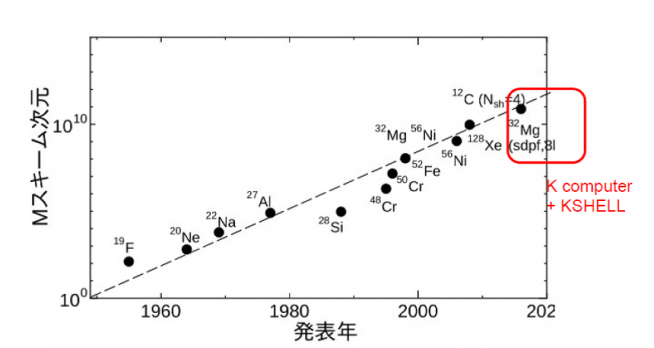
これほど速い計算コードを使えば、核子数の大きな原子核や、中性子過剰な不安定核まで幅広い研究が可能になります。世界中で大きな原子核の計算実績が積み上げられる流れの中で、清水さんはスーパーコンピュータ「京」とKSHELLコードを使って、752億次元の32Mgの原子核を、世界に先駆けて2017年に計算しました(図3)。現在、1000億次元を超えるような計算も完遂しています。
清水さんはKSHELLプログラムを誰でも使えるように公開しています*2。できるだけ簡便に使えるように工夫してあるので、理論研究者でなくても使いこなせます。学会で、実験研究者から「あのKSHELL計算コード使わせてもらっているよ。ありがとう」とお礼を言われることもあるそうです。
KSHELLコードを発展させ、未解決物理問題を解明
清水さんは計算方法のさらなる発展に挑んでいます。それは、核準位密度を求めるという応用を見据えた計算方法です。核準位密度とは、ある励起エネルギー領域に、どのくらいの数のエネルギー準位が存在しているかを密度で表した物理指標です。これは、元素合成過程などで現れる中性子捕獲反応などを理解するために重要な数値です。
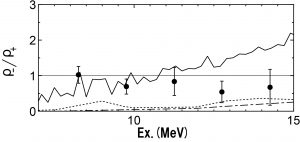
これまでの理論の先行研究では、実験で得られた核準位密度の一部を計算で再現できないという問題がありました。そこで、清水さんは、筑波大学の櫻井鉄也教授グループが開発した確率論的固有値密度推定法を殻模型計算に応用しました。スーパーコンピュータ「京」で150億次元の固有値密度を計算できるコードです。すると、次元を減らした近似では再現できなかった57Feの準位蜜度(実験値)を再現できる計算結果が得られました(図4)。
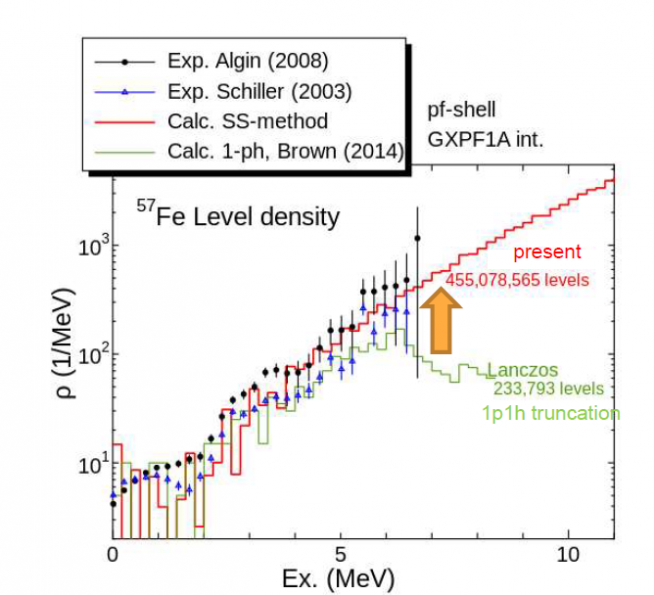
図4 確率論的固有値密度推定法を殻模型計算に応用した効果
横軸は励起エネルギー、縦軸は準位密度。57Feのデータ。●は2008年に、▲は2003年に発表された実験データ。実験データは励起エネルギーが高いほど準位密度が高くなる。本来は4.5億次元の行列の方程式を解く必要があるが、23万次元程度まで減らした近似を採用した計算結果が緑線であり、準位密度が低めにでてしまう。一方で、清水さんが計算した赤線は励起エネルギーが高い領域でも準位密度が下がらない。この計算手法では次元を減らす近似は必要なく、4.5億次元の計算ができる。清水さんの結果は実験データをよく再現しているし、理論的にも正しいと考えられる。
次に清水さんは、この固有値密度推定法を殻模型に応用した計算法で、58Niの計算に挑みました。というのも58Niの原子核には、実験値を再現できない固有値準位密度にまつわる問題があったからです。この計算は、閉殻からの励起を一部計算に取り込む必要があるため、57Feの100倍の計算量になります。
核子が入る軌道を特徴づけるのは、励起エネルギーとスピンとパリティです。パリティには+と-の2種類があります。 58Niでは、パリティが+と-の状態の準位密度はほぼ同じになるといわれていました。実際に、実験値では、ほぼ同じデータが観測されています。しかし、これまでの計算法(HFB法Hartree-Fock-Bogoliubov model)では、この状態を再現できていませんでした。「我々の開発した計算法を使うと、ほぼ同じであるという結果が得られました」と清水さんは成果を語ります(図5)。この計算では閉殻部の核子について一部の運動を計算に取りこむ必要がありました。さらに無視した部分の効果をどのように見積もるかにも清水さんの工夫が盛り込まれています。「多くの研究者が納得してくれるようにするのは苦労しました」と清水さんは言います。
スーパーコンピュータの性能があがれば、もっと核子数が大きい原子核も殻模型で計算できるようになります。「ポスト『京』では核子数が150~200くらいまでの計算ができるようになると嬉しいですね」と清水さん。清水さんの研究はポスト京重点課題⑨「宇宙の基本法則と進化の解明」にも選ばれています。計算機の性能アップと清水さんの研究がかけ合わさって、また新たな真実が明らかになっていくことでしょう。
*1:モンテカルロ殻模型計算は月刊JICFuS 2015年6月号 『大規模シミュレーションで核変換反応を明らかにする』で詳しく紹介されています。
*2 :https://sites.google.com/a/cns.s.u-tokyo.ac.jp/kshell/
関連記事
- 月刊JICFuS:発見から100年-原子核の謎に第一原理計算を駆使して挑む(2011/12/16公開)
- 月刊JICFuS:原子核の正体を解き明かす(2013/6/7公開)
- 月刊JICFuS:大規模シミュレーションで核変換反応を明らかにする(2016/1/18公開)
- 月刊JICFuS:原子核の基本的な性質を核力に基づいて解き明かす(2017/11/6公開)