原子核というと球形を想像し、実際に多くの原子核は球形です。ところが、ある種の原子核はミカンやラグビーボールのような楕円体などの形をとることがあります。東京大学大学院理学系研究科特任研究員の角田佑介（つのだ・ゆうすけ）さんは、このような原子核の変形を計算で解析することで、原子核の性質を解き明かそうとしています。
原子核は丸いもの？
原子の中心にある原子核は陽子と中性子の２種類の核子が集まってできています。原子核がばらばらにならないのは、核子の間に核力がはたらき、互いを束縛しているからです。原子核には特に安定となる陽子や中性子の数があり、魔法数といいます。安定な原子核は球形をしていますが、魔法数から離れると自発的に変形します。変形の種類にはミカン型（オブレート変形）やラグビーボール型（プロレート変形）などが知られており、原子核は変形すると回転し、異なった挙動をとります（図1）。
「私たちの研究グループが注目しているのは、天然に存在しないエキゾチック原子核です。中性子の数が過剰なエキゾチック原子核は不安定で、安定な原子核では考えられないような構造をもつことがわかっています」と角田さんは話します。
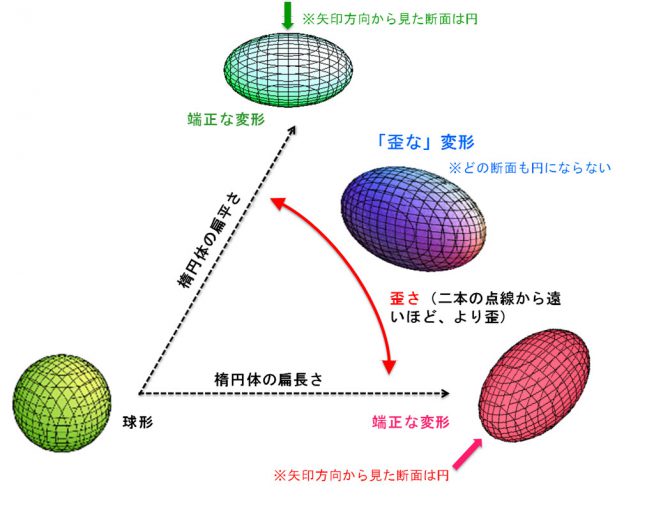
図1：原子核の形
原子核の基本的な形は、(1)球、(2)ラグビーボールのような扁長な回転楕円体（プロレート変形）、(3)みかんのような扁平な回転楕円体（オブレート変形）、(4)どれでもないいびつな形に分けられる。
【出典：https://www.s.u-tokyo.ac.jp/ja/press/2012/16.html】
エキゾチック原子核の計算が可能に
エキゾチック原子核は非常に寿命が短いのですが、近年の技術の進歩によって実験で作って観測ができるようになってきました。その結果、原子核の構造が変化する「殻進化」など、安定原子核とは異なる性質を示すことがわかってきました。そのため、エキゾチック原子核では、原子核の変形などさまざまな性質が異なると考えられます。しかし、エキゾチック原子核の構造や反応を実験だけで明らかにするのは困難です。そこで、理論計算が有効な手段になるのです。
原子核の性質を明らかにするために「殻模型計算」が使われます。原子核の中で核子はある軌道を回っており、その軌道が中心から殻をつくっていると原子核をモデル化し、この殻の中に核子を詰めたものとすると、原子核の性質を理解できます。殻模型計算では、殻構造をもとに理論計算を行います（図2）。
殻模型計算で原子核を調べる際には核子がどのような軌道を占有しているか、つまり核子の詰め方を考えます。詰め方はたくさんあり、できる限りすべてを使おうとすると計算の量が莫大になってしまいます。しかし、特に重要なものに詰め方を絞って計算するモンテカルロ殻模型法を使うと、計算量が節約できます。
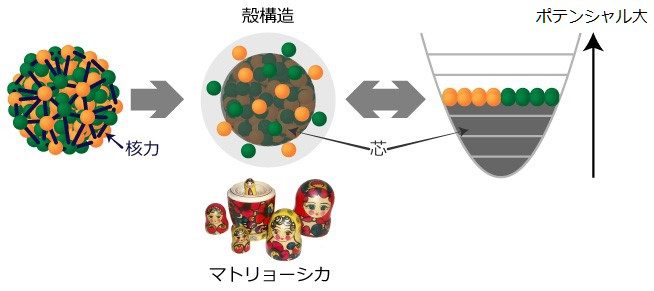
図2：殻模型
原子核は核子どうしが核力により全体を形作っている。核力の性質は複雑だが、原子核は殻の構造の中に核子を詰めていったものとする殻模型を使うと、原子核の多くの性質が理解できる。殻構造を核子全体がつくるポテンシャルのくぼみの中に核子が閉じ込められた状況として、殻構造を計算する。
エキゾチック原子核では、通常の安定な原子核で確立していた殻構造が壊れて、新たな殻構造が現れます。そのため、エキゾチック原子核の計算には多くの軌道を考慮する必要があります。
「エキゾチック原子核の計算は、従来の殻模型計算でやるのには制約があります。そこで、モンテカルロ殻模型法を使い、さらにスーパーコンピュータを駆使することにより計算を実現しました。こうして、原子核の変形を理論的に調べることができるようになりました」と角田さんは説明します。
エキゾチック原子核における殻構造の変化のメカニズムは核子間の相互作用にあります。そこで、モンテカルロ殻模型法でもこの相互作用を考慮して計算します。
角田さんは、原子核のpf殻に2つの軌道を加えた模型空間での計算にチャレンジしました。まずは共同研究者が開発した相互作用を用いて計算し、エキゾチック原子核の計算が実現できました。計算結果を既存の実験データと比較したところ、精度の高い計算結果が得られたおかげで、計算に必要な有効相互作用の精度が不十分なことが判明。角田さんは、計算結果が実験データを再現できるように有効相互作用を改良しました。
こうして、改良した有効相互作用を用いて、ニッケル（Ni）同位体の原子核において、殻模型計算を行いました。さらに、この結果を解析して、モンテカルロ殻模型の波動関数から原子核の形状の情報を抽出し、変形の状態を可視化する方法を考案しました（図3）。
「計算で出てくる結果から原子核の変形の程度を白丸で示し、大きい白丸の集まっている領域を見ると、各エネルギー状態に対応する原子核の形状がわかります。この可視化法をT-plotと名付けました」。
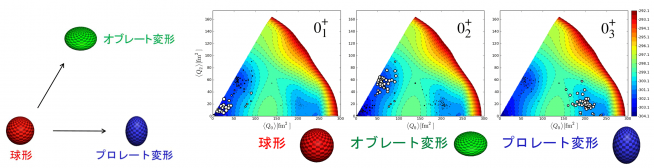
図３：ニッケル68の原子核の形状の解析
変形度（左図）に対するエネルギーの変化を色で示した図に、波動関数の成分を白丸でプロットした（右図）。エネルギーは青が低く、赤が高い。大きい白丸の集まっている領域を見ると、各状態に対応する原子核の形状がわかる。
異なる形の原子核が共存するニッケル同位体
ニッケルの陽子数は28で魔法数に一致する原子核であるため、基底状態は安定で、球形をしています。しかしニッケルには多くの同位体があり、中性子の数が過剰なエキゾチック原子核では、変形しているエネルギー状態が現れると考えられます。
角田さんはニッケル同位体の励起エネルギーなどの性質を計算により再現し、T-plotを用いることで、中性子数が40のニッケル68に球形、ミカン型、ラグビーボール型の3種類の異なる変形状態が共存していることを予言しました。さらに変形が共存する理由を「第2種殻進化」という新たな概念で説明しました。
先に述べたように、殻構造が変化することを殻進化といいます。これまで知られていた殻進化は、陽子数や中性子数が変化することで起こるもので、異なる核種で殻構造が変化します。これを「第1種殻進化」とし、これに対し新たに提唱された「第2種殻進化」は、同一の核種で殻構造が変化するものです。原子核の形状や核子の配置の変化に伴い、殻構造が動的に変化するというメカニズムを考えると変形共存が説明できます。「これは核子どうしではたらくテンソル力が殻の構造を変化させるという性質を用いることで説明できました」と角田さん。
理論から原子核の性質を解き明かす
モンテカルロ殻模型法や角田さんが開発したT-plotの計算で、エキゾチック原子核の変形共存が明らかになりました。さらに計算を進め、ニッケル70でも3種類の変形共存が予言され、変形状態はエネルギーが低く、より安定していることがわかりました。また、中性子をもっと増加させたニッケル78では球形のみが安定となり、形の共存は失われるという結果も得ています（図4）。
「ニッケル同位体の変形共存は実験的にはまだ完全には確かめられてはいません。変形状態を明らかにするため実験グループとの共同研究を積極的に進めており、ニッケル70では変形状態と考えられる低いエネルギー状態があるという予言通りの実験結果が得られました。これは、変形共存の研究において大きな意義があります」。
原子核の形は、ミカン型やラグビーボール型のみならず、バナナ型や正四面体型など新奇なさまざまな形があると理論的に予想されています。また、原子核の形状の研究は、宇宙の核反応の性質の説明にもつながります。
角田さんは「形状の変化で原子核の性質がわかるのがおもしろい」と話します。「原子核は、量子力学で記述されるミクロな物理系である一方、形のようにマクロで直感的な性質も持ち合わせています。両方の見方から研究できるのもこの研究のおもしろいところ。計算からどんな原子核の性質が明らかになるのか興味はつきないです」。この研究成果が認められて第11回（2017年）日本物理学会若手奨励賞を受賞した角田さん。今後も意欲的に研究を進めていきます。
図４：ニッケル同位体の変形
変形度（左軸がミカン型、右軸がラグビーボール型）と束縛エネルギー（縦軸）を示した。中性子数が少ないニッケル68、70は球形、ミカン型、ラグビーボール型が共存しているが、中性子数が増えてニッケル74、78になるとエネルギー状態が変わり、ニッケル78では球形のみが存在して形の共存が失われることがわかる。エネルギーの低いところに変形状態が現れる。
