JICFuSでは、これまで進めてきたポスト「京」重点課題(9)「宇宙の基本法則と進化の解明」での研究成果を引き継ぎ、2020年度より、「富岳」成果創出加速プログラム領域①「人類の普遍的課題への挑戦と未来開拓」を実施しています。同領域では「シミュレーションで探る基礎科学：素粒子の基本法則から元素の生成まで」および「宇宙の構造形成と進化から惑星表層環境の変動までの統一的描像の構築」の2課題を設定。そのうち、「シミュレーションで探る基礎科学：素粒子の基本法則から元素の生成まで」では、「β中間子崩壊」「QCD相構造」「バリオン間力」「核構造とf過程」「中性子星合体」「時空生成」という6つの研究テーマに取り組んでいます。
今回は6つの研究テーマのうちの「時空生成」について、KEKの畠山洸太さんたちが進めている「超弦理論の数値シミュレーションによる時空創発の研究」を紹介します。
「超弦理論」とは何か
まず、「超弦理論」とは何かから簡単に説明していきましょう。超弦理論は「超ひも理論」とも呼ばれる現代物理学の理論の1つで、物質の最小単位である素粒子は、粒子ではなく、長さをもつ弦（ひも）であるというものです。現在、宇宙誕生のメカニズムや素粒子の成り立ちを説明する理論の有力な候補の1つとして、世界中で研究が進められています。
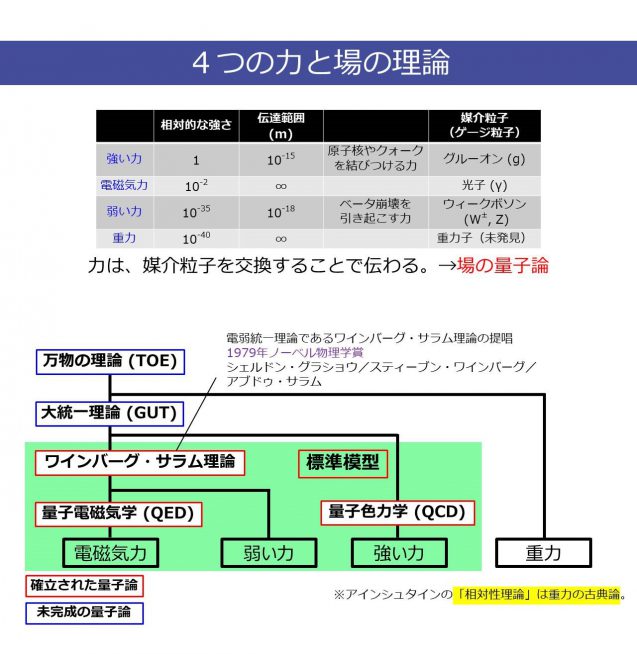
ミクロの世界を記述する理論は「量子論」と呼ばれています。量子論の1つである超弦理論が登場する以前、量子論では、素粒子を、大きさをもたない点粒子として扱ってきました。自然を支配する力には、強い順に「強い力」、「電磁気力」、「弱い力」、「重力」という4つがあります。強い力は原子核を構成する陽子と中性子の中のクォークと呼ばれる素粒子同士がグルーオンと呼ばれる素粒子を受け渡すことで伝わる力です。電磁気力は電子同士が光子（光の素粒子）を受け渡すことで伝わる力です。そして、弱い力はニュートリノと呼ばれる素粒子が電子やクォークに接近したときなどにウィークボゾンと呼ばれる素粒子を受け渡すことで伝わる力です。一方、重力は重力子（グラビトン）と呼ばれる素粒子によって伝わる力だと考えられていますが、現時点では観測されていません。力の受け渡しに関わる素粒子を「ゲージ粒子」と呼び、力が粒子の交換で伝わるとする理論を「場の量子論」と呼びます。
重力を除く3つの力に関しては、場の量子論に基づく「標準模型」で矛盾なく記述することができます。しかし、「一般相対性理論」で扱う重力は記述することができていません。そのため、量子論と一般相対性理論の両方を矛盾なく記述できる理論の構築が、理論物理学者にとって大きな課題となっていました。そこで、考え出されたのが、素粒子を長さだけをもつ弦の振動として表す超弦理論でした。 超弦理論における弦には、「閉じた弦」と「開いた弦」の2種類があり、開いた弦は重力子以外のゲージ粒子を、閉じた弦は重力子を含んでおり、4つの力を記述できることから、「万物の理論」となりうる可能性を秘めているのです（図1）。
図1：4つの力と場の理論の関係
数値シミュレーションにより超弦理論を検証
現在、超弦理論には5つのバージョンがあり、それぞれ「タイプⅠ」「タイプⅡA」「タイプⅡB」「ヘテロSO（32）」「ヘテロE8×E8」と呼ばれています。 これらの超弦理論には、理論の整合性を図るため、9次元空間に時間を加えた10次元時空が必要です。
一方で、我々は縦・横・高さの3次元空間に時間を加えた4次元時空しか認識することができません。我々が認識できない残りの6次元空間は「余剰次元」と呼ばれ、量子レベルでコンパクト化されていると考えられています。また、以前、超弦理論の5つのバージョンは、それぞれ別々の理論であると見なされていましたが、1995年に、これら理論はすべて等価であり、超弦理論に1次元加えた11次元時空を必要とする「M理論」に統合できるという考えが提唱されました。現在、M理論を含む6つの理論は、「双対性」によって互いにつながっていると考えられています。
超弦理論における弦の大きさは10-35メートルと極めて小さく、これを観測するには、1016TeV（テラ電子ボルト）という超高エネルギーが必要です。しかし、現在の科学技術ではこのような超高エネルギーを出力することは不可能なことから、超弦理論を直接検証することは非常に困難と考えられています。そこで、実験の代わりにスーパーコンピュータを使った数値シミュレーションにより、検証しようという試みが世界中で進められています。
日本において、その中心的役割を担ってきた本研究グループでは、ポスト「京」重点課題(9)「宇宙の基本法則と進化の解明」において、スーパーコンピュータ「京」を使い、超弦理論の「タイプⅡB」を基に、数学の「行列」を使った「タイプⅡB行列模型」（図２）と呼ばれるモデルによる数値シミュレーションを実施してきました。
図２：「タイプⅡB行列模型」は次のような式で表される。この模型では時空は行列の自由度からダイナミカルに創発される。
超弦理論が万物の理論であるならば、現時点で得られている標準模型や一般相対性理論、宇宙論で説明されている物理を超弦理論の行列模型は再現するはずです。そこで、本研究グループでは、現時点で得られている物理を行列模型のシミュレーションによって再現できるかどうかを調べているのです。ちなみに、もし「タイプⅡB行列模型」で超弦理論が検証できれば、等価である他の4つのバージョンについても同時に検証できたことになります。
まずは、その具体的な内容を簡単に紹介し、その上で、現在の研究内容を紹介していくことにしましょう。
初期宇宙を数値シミュレーションしインフレーションを再現
さて、冒頭で、超弦理論は「宇宙誕生のメカニズムや素粒子の成り立ちを説明する理論の有力候補の1つである」と紹介しました。これはどういう意味でしょうか。
宇宙は約138億年前に誕生し、ある1点から始まり、膨張を続けながら現在に至っていることが観測結果などから明らかになっています。誕生した宇宙は、その直後の10-36～10-34秒の間に、指数関数的に膨張するインフレーションを起こし、さらにインフレーション後、超高温・高密度のエネルギーの塊が発生し、ビッグバンが起こったと考えられています。宇宙の始まりからビッグバンの前後までを「初期宇宙」と呼びます。
ビッグバン以降の時空に関しては、場の量子論と一般相対性理論を使って、非常によく説明することができます。ところが、素粒子がバラバラで、自由に動き回っていたと考えられる初期宇宙に関しては、場の量子論と一般相対性理論では、説明することができません。これは、宇宙が始まりインフレーションが終わるまでの短い間に、「自発的対称性の破れ」が起こり、それにより元々あった10次元時空から4次元時空が誕生し、残りの6次元（余剰次元）はコンパクト化し、現在の素粒子が作られたということを示唆しているのです。
そこで、これまで本研究グループでは、初期宇宙において、超弦理論で予想される10次元時空から、一体どのように4次元時空が誕生したのかを説明するため、スーパーコンピュータ「京」を使った数値シミュレーションに取り組んできました。それにより、時空の時間発展を再現し、超弦理論を検証しようというわけです。具体的には、行列を碁盤の目のように小さく分割し、できた小さな行列を並列計算機の各計算ノードに割り当てることで、並列計算を実行しました。数値シミュレーションの結果からは、小さな10次元時空（9次元空間＋時間）から、自発的対称性の破れが起こって4次元時空（3次元空間＋時間）が生まれ、そのうち3次元空間が、時間とともに指数関数的に膨張し始めていることが確認されました。これは、宇宙の始まりからインフレーションまでの時期に対応しています。さらに、時間発展を見ていったところ、指数関数的な膨張はある時点で止まり、そこから先は、時間とともに時間の2分の1乗で膨張していることが確認されました（図３）。
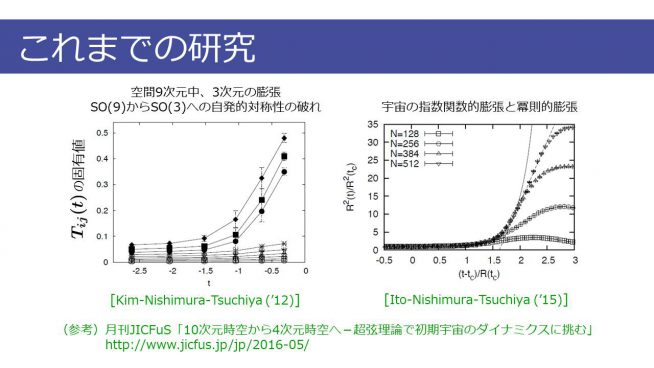
図３：これは数値シミュレーションにより得られた結果を座標にプロットしたもの。横軸に時間、縦軸に残りの9次元空間の各方向の広がり（空間のスケール）を取っている。この図からは、最初の時点では、9つの点がすべて小さな値を取っていることがわかる。これは、この時点では9次元空間は非常に小さくつぶれており、まだ3次元空間が誕生していないことを表している。しかし、時間発展を見ていくと、ある時刻を境につぶれていた9次元空間のうち、3次元空間だけが、指数関数的に膨張を始めた。さらに、時間発展を見ていくと、指数関数的な膨張はある時点で止まり、そこから先は、時間とともに時間の2分の1乗で膨張していることが確認された。
「符号問題」を克服するため「複素ランジュバン法」を適用
しかし、ここでは、ある“近似”を用いた数値シミュレーションを行っていました。それは、「符号問題」（あるいは複素位相問題）と呼ばれる問題を回避するためです。符号問題は理論物理学におけるさまざまな場面で現れ、大きな課題となっています。特に符号問題により、場の量子論を非摂動的に研究するための強力なツールであるモンテカルロシミュレーションを使うことができないため、量子色力学の相図を第一原理計算により解くことができないなどの問題が発生しています。符号問題の解決は、理論物理学における大きなブレークスルーとなります。そのため、現在、符号問題を克服するためのさまざまな方法が考案されており、その1つに「複素ランジュバン法」があります（図４）。
図４：「複素ランジュバン法」は符号問題を克服するための方法の1つ。
そこで、本研究グループは、「富岳」成果創出加速プログラム領域①の下、「シミュレーションで探る基礎科学：素粒子の基本法則から元素の生成まで」において、複素ランジュバン法を、「タイプⅡB行列模型」の数値シミュレーションに適用することで、符号問題の克服に取り組むことにしました。
「ただし、従来であれば、10次元時空（9次元空間＋時間）の数値シミュレーションを実行したいところでしたが、今回は計算資源の関係から、まずは、ボーズ粒子（例えば、ゲージ粒子やヒッグス粒子 ）のみを含む10次元時空の『タイプⅡB行列模型』の数値シミュレーション を実行しました。使用した主なスーパーコンピュータは東京大学のOakbridge-CXです」（畠山さん）
行列サイズは大きくすればするほど、時空を微細化でき、無限大に近づけていくことで、素粒子の弦の描像を得ることができるようになります。そこで、行列サイズを1024×1024として数値シミュレーションを行いました。
確認できなかった「自発的対称性の破れ」
今回得られた数値シミュレーションの結果は、図の通りとなりました。
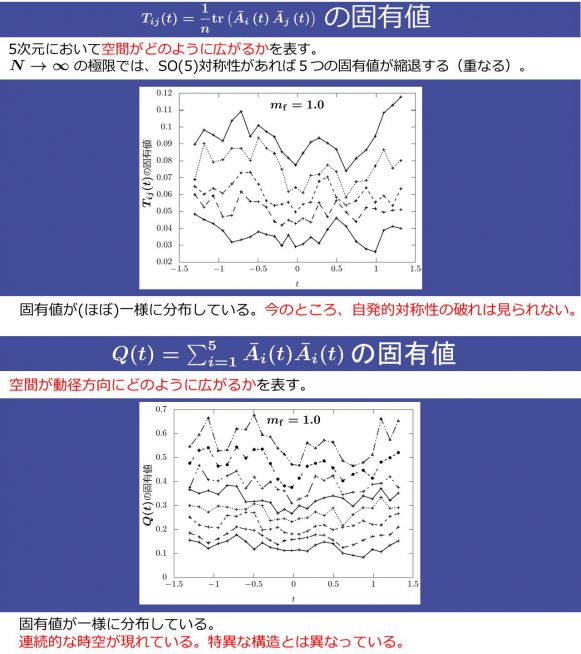
「本数値シミュレーションでは、時間発展とともに、9次元空間がどのように膨張するかを再現しました。本来であれば、9つの固有値のうちの3つのみが大きくなっていく様子、すなわち3次元空間のみが自発的対称性の破れ により、膨張していく様子を確認する予定でした。しかし、図からは、度合いは小さいものの、膨張する振る舞いを示す連続的な空間 は現れましたが、9つの固有値はすべてほぼ一様に分布しており、残念ながら、自発的対称性の破れを 確認することはできませんでした」（畠山さん）
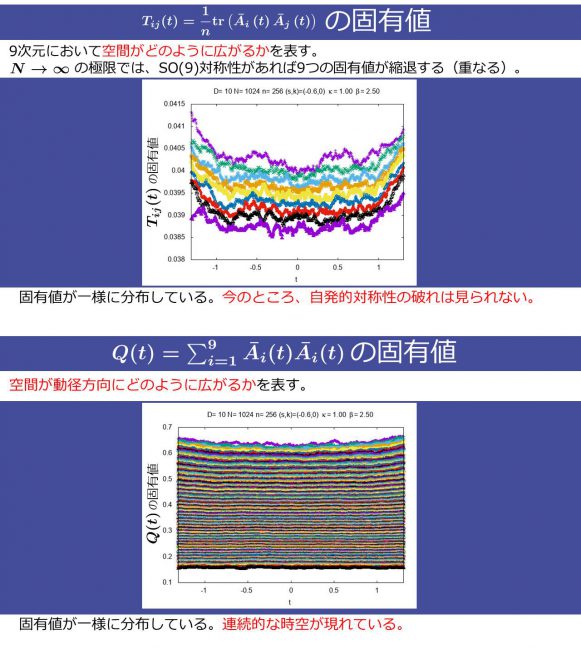
複素ランジュバン法を適用した10次元時空のボーズ粒子のみを含む「タイプⅡB行列模型」を使った数値シミュレーション結果。度合いは小さいものの、膨張する振る舞いを示す連続的な空間は現れているが、自発的対称性の破れは確認できなかった。
さらに、フェルミ粒子（例えば、クォークや電子などのレプトン ）とボーズ粒子の両方を含む「タイプⅡB 行列模型」のシミュレーションも行いました。ただし、フェルミ粒子を加えたため、6次元模型、かつ行列サイズを32×32と小さめに設定しました。それによって得られた数値シミュレーションの結果は図の通りです。しかし、この結果からも連続的な空間 が現れていることは確認されたものの、空間が膨張する振る舞いや自発的対称性の破れ を確認することはできませんでした。
6次元の「タイプⅡB行列模型」を使った数値シミュレーション結果。5次元空間はすべてほぼ一様に分布しており、連続的な空間が現れてはいるものの、空間の膨張や自発的対称性の破れは確認できなかった。
今後の「富岳」での取り組みと超弦理論の検証へ期待
フェルミ粒子とボーズ粒子の両方を含む「タイプⅡB行列模型」 のシミュレーションで得られた結果について、畠山さんは次のように述べています。「まず、今回のシミュレーションで連続的な時空が得られたことは、我々の住む宇宙を再現するために極めて重要なことです。連続的かつ膨張する空間と自発的対称性の破れを実現するためには、シミュレーションで設定するパラメータの値を適切に選ぶこと、そして、行列サイズNを大きくすることが必要だと考えています」
今後、本研究グループでは、これらの原因に取り組むと同時に、計算性能が桁違いに高い「富岳」を使い、10次元時空のフェルミ粒子とボーズ粒子の両方を含む「タイプⅡB行列模型」による数値シミュレーションを実行する計画です。この数値シミュレーションにより、自発的対称性の破れを確認することはできるのか、また、それによって発生した3次元空間はどのような膨張のしかたをするのか、さらには、余剰次元の構造がどうなっているのかを確認できるのかなどを検証していく計画です。それにより、標準模型や一般相対性理論で説明されている物理が超弦理論を使って再現できるのかを調べていきます。将来、数値シミュレーションの結果と観測結果を比較できるようになれば、超弦理論が万物の理論であることが明らかになるかもしれません。
