クォーク同士の相互作用のシミュレーション
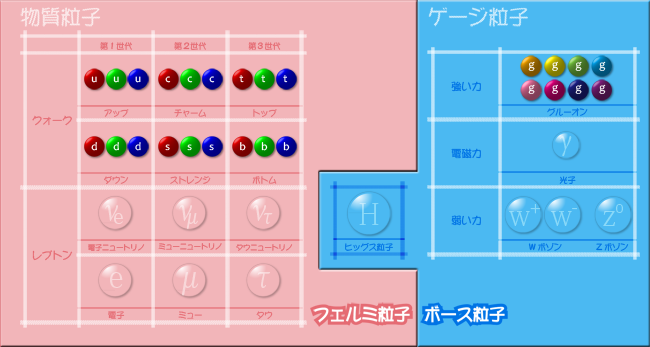
まずはおさらいから始めましょう。原子は原子核と電子でできています。原子核は陽子と中性子で構成されており、陽子と中性子はクォークと呼ばれる基本粒子で構成されていることが知られています。クォークは6種類あります。一方、電子には同様の性質をもつものがほかに2種類存在し、これらに3種類のニュートリノを合わせたものをレプトンと呼んでいます。このクォークとレプトンが、物質を構成する粒子であるフェルミ粒子です。フェルミ粒子の間に働く力は、4種類のボース粒子（グルーオンなどのゲージ粒子）によって媒介されると考えられています（図1）。
図1：素粒子標準模型に含まれる17種類の素粒子（クレジット：高エネルギー加速器研究機構）
さて、これらのフェルミ粒子とボース粒子の運動は、「素粒子標準模型」によって記述することができ、理論的にも実験的にも正しいことがわかっています。しかし、クォークの運動の力学については、いまだに理解が進んでいません。これを解明するためには、素粒子標準模型に基づいてクォーク同士の相互作用を計算する必要がありますが、この計算が難しいのです。そこで、原子核内のクォーク同士の相互作用を、スーパーコンピュータによるシミュレーションで解明しようとしているのが、広島大学大学院理学研究科の金森逸作（かなもり・いっさく）さんです。
金森さんはこう話します。「現在、主流となっている計算手法は『格子定式化』です。ところが、クォーク同士の相互作用を『格子定式化』を用いたシミュレーションできちんと取り扱おうとすると、膨大な計算量になってしまいます。そのため、以前は、クォークの効果を部分的にしか取り入れない近似計算が行われていたほどです。それでも格子定式化を使っている理由は、計算による発散をうまく扱うことができることと、原理的に近似計算をせずに済むことの2つの利点があるからです。とくに2つ目については、たとえば電子の記述で成功を収めている摂動近似を使ってしまうと、クォークが3個集まってできる陽子の存在自体を説明できなくなるのです。」
格子定式化とは、一体どのような手法なのでしょうか。それは、空間を正方形の格子状に切っていき、それぞれの格子点にクォークを定義し、格子点と格子点を結ぶ線にクォーク同士を結びつけるグルーオンを定義するというものです（図2）。
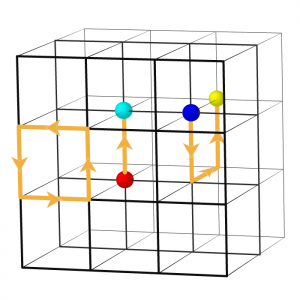
図2：格子定式化
空間を格子状に切り、それぞれの格子点にクォーク（着色された球）を、格子点同士を結ぶ線にクォーク同士を結びつけるグルーオン（黄色矢印）を定義する。（クレジット：高エネルギー加速器研究機構）
格子点と格子点を結ぶ線の長さをパラメータの1つとしてゼロに近づけていくこと、すなわち限りなく小さくしていくことを「連続極限を求める」といいます。我々の知る時空間は格子ではないので、最後に連続極限を求めることによって、クォーク同士の相互作用の計算が完了します。また、クォークとグルーオンの基礎理論は、標準模型のなかでも特に「量子色力学（QCD）」と呼ばれていることから、このような格子上でQCDを扱うことを「格子量子色力学（格子QCD）」と呼びます。
スーパーコンピュータに最適なプログラムを開発
現在、金森さんは、スーパーコンピュータ「Oakforest-PACS（OFP）」（図3）を使って、クォーク同士の相互作用を計算するプログラムやアルゴリズム、コードの開発を進めています。
図3：東京大学情報基盤センターと筑波大学計算科学研究センターが共同運用する最先端共同HPC基盤施設（JCAHPC）のスーパーコンピュータ「Oakforest-PACS（OFP）」
スーパーコンピュータの性能ランキングTOP500において、2016年11月に国内1位を獲得。ピーク性能はスーパーコンピュータ「京」の2.2倍。（クレジット：最先端共同HPC基盤施設）
「Oakforest-PACSは、現在、日本で最も高性能なスパコン（スーパーコンピュータ）の1つです。しかし、どんなスパコンであっても、適したプログラムを開発しなければ性能を十分に生かすことができないため、現在はもっぱらその開発に注力しています。開発したプログラムをOakforest-PACSに合わせてチューニングすることにより、従来のプログラムをそのまま実行するのと比べて3～5倍以上の計算量を実行できるようになると見込んでいます。それにより、計算時間の短縮はもちろんのこと、消費電力やコストを大幅に削減することができます。その結果、削減分を他の数値計算に回すことができるので、競争優位性を確保できるというわけです（図4）」と金森さんは語ります。
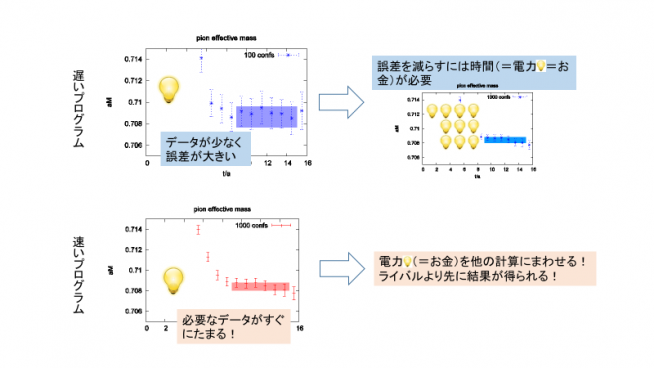
図4：速く計算できるプログラムの開発
それぞれのスーパーコンピュータに適したプログラムを開発して計算速度を上げることで、計算時間の短縮、消費電力やコストの大幅な削減が見込める。削減分を他の計算に回すことができるため、研究の競争優位性を確保できる。（クレジット：金森逸作、作図協力：広島大学大学院理学研究科博士課程・上野崚一郎氏）
具体的にはどのようなチューニングを行っているのでしょうか。金森さんは、「プログラムでは大きな行列式の掛け算を繰り返すことになるのですが、その掛け算のやり方を工夫することで、高速化を図っています。また、スパコンに合わせたデータ構造にする必要もあります。スーパーコンピュータ「京」もOakforest-PACSも超並列型で、特にOakforest-PACSの場合、計算ノード（計算機の最小単位）が8208台あり、しかも1つのノードに計算コア（実際に計算する部品）が68個もあるため、いかに計算ノードをフル活用しつつ、ノード間の通信時間を短縮するかがポイントになります」と言います。
加えて、クォークの相互作用を解くプログラムは、国内外を含め多くの研究グループが開発しています。そのため、他の研究グループが開発したプログラムと金森さんの研究グループが開発したプログラムを組み合わせて使うといった場合もあります。「したがって、他の研究グループのプログラムをOakforest-PACS向けにチューニングしたり、足りないプログラムを新たに開発したりといったことも行っています」と金森さん。
さらに現在は、ポスト「京」コンピュータに向けたプログラム開発も進めています。計算性能がさらに向上することにより、格子の幅をより狭く、扱う空間をより広く、そして、扱うクォークの種類も増やせるようになります。
格子定式化との出会いと超対称性の自発的破れ
実は金森さんは元々プログラム開発の専門家ではなく、素粒子物理学の研究者です。そんな金森さんがスーパーコンピュータのためのプログラム開発に着手することになったきっかけは、大学院生時代に場の量子論の格子定式化に興味を抱いたことにありました。
「場の量子論の格子定式化には、量子ゆらぎに由来する発散を正則化できる上、近似計算を経由せずに理論を定義できるというメリットがあります。そこで、私は大学院時代、“超対称性”の格子定式化に取り組みました。超対称性は、場の量子論の中でも格子定式化が十分に行われていなかったものの1つだったからです。超対称性の格子定式化への挑戦を決意した背景には、あわよくば、超弦理論のような究極理論への1つの足がかりが得られるのではないかという期待もありました」。金森さんはこう振り返ります。
超対称性とは、フェルミ粒子とボース粒子を入れ替えても理論が変わらないというものです。しかし、実際の世界では、フェルミ粒子とボース粒子は重さがまったく異なるため、超対称性はそのままの形では実現していません。つまり、超対称性は自発的に破れていると考えられているのです。とはいえ、このシナリオを確認するには、超対称性が本当に自発的に破れているかどうかを調べる必要があり、そのためには、理論の近似計算を経由せずに方程式を解かなければなりません。ここで着目したのが、原理的に近似計算を避けられる格子定式化でした。
当時、格子定式化はすでに「ゲージ理論」と呼ばれる種類の理論（QCDもそのひとつ）に使われており、それを用いたコンピュータ・シミュレーションが成功を収めていました。これは時間と空間を格子状に切って、コンピュータ上に理論をのせるというものです。一般に、場の理論を格子上で扱ったものは「格子場の理論」といいますが、ゲージ理論を格子上で扱うのが「格子ゲージ理論」、とくにQCDを格子上で扱うのが、前半に出てきた「格子QCD」というわけです。
しかし、残念なことに、一般に格子定式化は超対称性を本質的に壊してしまうため、超対称性をもった理論を、格子QCDのようにシミュレーションすることは不可能と考えられていました。
それに対し、2008年当時、理化学研究所仁科加速器研究センターに在籍していた金森さんの研究グループは、その少し前に提唱された超対称性と相性の良い定式化に着目しました。そして、その格子定式化に基づき、超対称性の自発的破れを測る指標である真空エネルギーをシミュレーションするプログラムを開発。さらに、それを理化学研究所のスーパーコンピュータ「理研スーパーコンバインドクラスター（RSCC）システム」を使って計算した結果、超対称性をもっている場合、真空エネルギーの値はゼロであることから、1次元空間のある超対称ゲージ理論では、超対称の自発的破れは起きていないという兆候を得ることに成功したのです。これは、超対称ゲージ理論での超対称性の自発的破れに関する世界初のシミュレーションとなりました。
ポスト「京」では超弦理論にも挑戦
「その後、縁あって、クォークとグルーオンの間の強い相互作用を扱うQCDのスーパーコンピュータによるシミュレーションに携わることになったわけですが、改めて、自分の研究者人生を振り返ると、一貫して、超対称性においてもQCDにおいてもその扱いが鍵を握るフェルミ粒子と格子が、私の研究の中心テーマであったことに気付きます。今後、ポスト『京』では、QCDに留まらず、B中間子、陽子や中性子など核子の間に働く核力、超対称性、さらには超弦理論においても格子定式化によって素粒子を定義し、スパコンで計算できるようにしたいと思っています。それにより、何か新しい物理が見つかることを大いに期待しています。そのための努力は惜しみません」。金森さんは力強くこう語りました。
