原子核の基本的な性質を核力に基づいて解き明かす

陽子や中性子からなる原子核は、物質の基本要素として重要です。しかし、原子核を形作る基本的な力「核力」には未知な点が多く、原子核の本質的な理解を妨げています。東京大学大学院理学系研究科の宮城宇志（みやぎ・たかゆき）さんは、核力から原子核を理解しようと計算手法を開発しています。

原子核を作っている力

原子核は、いくつかの核子（陽子と中性子）が「核力」によって結合することで作られています。核力は核子間に働く力のことで、陽子や中性子が接近したときに働きます。電磁気力にくらべてはるかに強い力のため、陽子同士に働く電気的な斥力に逆らって原子核を結合させることができます。
核力は、1935年の湯川秀樹による「中間子論」に基づいて理解されてきました。これは、2つの核子の間で中間子が交換されることによって核力が生じるというものです。さらに、その後の主に加速器を用いた核子散乱の実験で、核子間の距離が近づく（10^-15m以下）と、強い反発力（斥力芯）が生じることもわかりました。
量子色力学（QCD）の発展から、核子や中間子はクォークとよばれる素粒子と、それを結び付けているグルーオン（糊粒子）からなる複合系であることが明らかになりました。複合系であるため、核子間の相互作用は非常に複雑で、特異な性質を示します。核力を理解することは難しく、不明な点がまだたくさんあるのです。

2体力から3体力へ

原子核は、核力を及ぼし合う多数の核子から構成される多体系です。これまで、現象論的な核力に基づく原子核の研究では、主に2つの核子の間に働く力である2体力が使われてきました。ところが、近年になって計算機の性能が大幅に向上し、精度の高い計算が行われるようなると、理論計算と実験や観測値との間に大きな差が生じ、2体力だけではその差を説明できなくなりました。そのため、3つの粒子間に働く3体力のような多体力を考慮することが重要だと指摘されるようになりました。
3体力は2体力に比べて実験的に検証するのは難しく、高速な計算機によりようやく計算が始まったところです。現在は、核力によって原子核や核物質を統一的に理解しようとする研究が進んでおり、そのためにも、3体力を含めた核力の解明が求められています。

原子核の飽和性を再現する

東京大学大学院理学系研究科の宮城宇志さんは、核力によって原子核を理解しようと研究しています。安定な原子核には「飽和性」と呼ばれる2つの基本的な性質があります。ひとつは、１核子あたりのエネルギーは核種によらずほぼ一定である（結合エネルギーの飽和性）ことです。もうひとつは、原子核の中心密度は核種によらずほぼ一定（密度の飽和性）で、原子核の半径は（核子数）の1/3乗に比例することです（図1）。
飽和性は安定原子核においては普遍的な性質であり、実験的には古くから知られています。しかし、核子間の相互作用に基づいて理論的に説明できるかどうかはまだわかりません。そこで、宮城さんは「数値計算によって核力から原子核の飽和性を再現し、多体系としての原子核の性質を解き明かしたい」と、計算手法を開発しています。

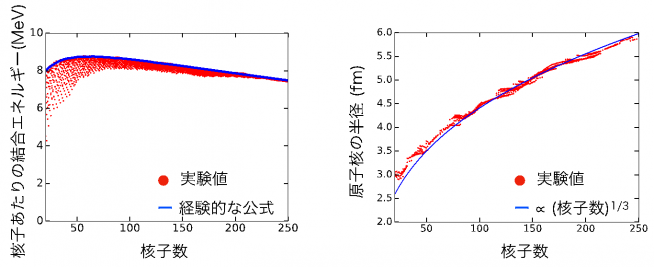
図1：原子核の飽和性
（左）結合エネルギーの飽和性：１核子あたりのエネルギーは核種によらずほぼ一定。（右）密度の飽和性：原子核の半径は（核子数）の1/3乗に比例する。赤点は実験データ、青線は経験的な公式により得られる。エネルギーの実験値は、M. Wang et al., Chin. Phys. C36, 1603 (2012)、半径の実験値はI. Angeli and K. P. Marinova At. Data Nucl. Data Tables 99, 69 (2013)から引用。

どの核力を使うか

核力は、その起源である強い相互作用の理論「QCD」から、原理的には計算することができます。ところが、QCDの第一原理計算には膨大な計算能力が必要で、スーパーコンピュータを用いた核力の導出は現在進行中の非常に難しい問題です。そのため、低エネルギー領域の原子核を扱う数値計算では、現象論的な模型を用いるのが主流です。
現象論から与えられる核力にはいくつかの模型があるのですが、宮城さんは主にカイラル有効場の理論による核力を用いることにしました。「カイラル有効場の理論は、QCDの低エネルギー有効理論です。摂動の高次項を取り入れることによって多体力を取り扱えるとともに、核力を系統的に理解できる可能性があります」と宮城さんは説明します。
この核力を用いて、シュレディンガー方程式によって2重水素や3重水素など軽い原子核の基底状態エネルギー^※1を直接対角化法で計算しました（図2）。「その結果わかったことは、核子の数が増えると計算が大変になることと、収束にいたるまでに大きな模型空間^※2が必要なことでした。このままではもっと重い原子核は計算できません」。

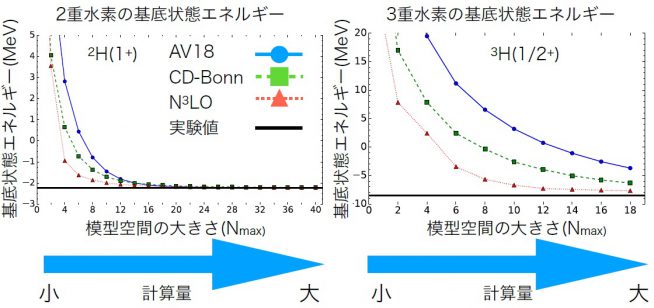
図2：水素同位体の基底状態エネルギーを計算した結果
カイラル有効場理論による2核子間相互作用（N³LO）と、その他のよく使われる相互作用（AV18とCD-Bonn）を使った。2重水素にくらべ、3重水素は計算量が多く、収束した解を得るためにはさらに大きな模型空間が必要となる。

UMOAによる計算へ

そこで、これらの問題を解決するための方法を検討しました。まずは、計算するのにどうして大きな模型空間が必要になるのかを考えました。「そもそも相互作用は、エネルギーや半径のような物理量ではありません。なので、物理量を変えずに、模型空間を小さくできるように相互作用を変換してやればよいのです」と宮城さん。相互作用を変換する方法にはいくつかあるのですが、多体力を計算することを考慮し、相似くりこみ群（SRG）という方法を使うことにしました。SRGによって変換した核力を使えば、小さい模型空間でも収束した答えが得られ、計算をスピードアップさせることができました。
では、核子の数が増えたときにはどう計算するか。もっと重い原子核になれば、計算量は莫大になります。そこで使ったのがユニタリ模型演算子法（UMOA）という方法です。「この方法では、重要と思われる自由度についてのみ計算を行うので、重い原子核についても計算可能です」と宮城さんは続けます。UMOAでは、計算に必要なハミルトニアン（系全体のエネルギーを示す関数）を変換し、基底状態について重要と考えられる相関を取り入れます。この方法はエネルギー以外の物理量を容易に計算できるという利点があり、結合エネルギーだけでなく半径も計算することができます。

3体力の効果が必要

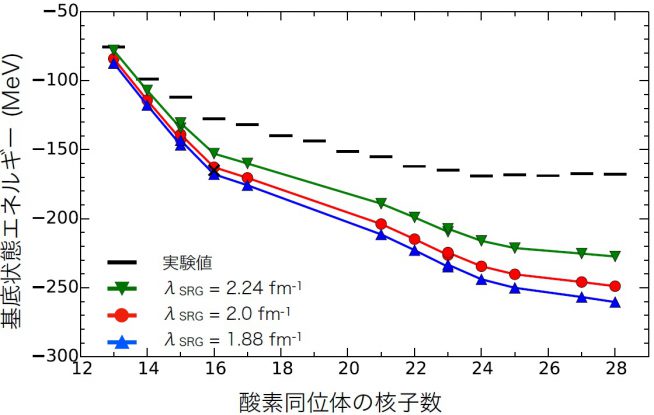
まずは、2体力の核力で系統的な計算を試みました。UMOAでヘリウム4の基底状態エネルギーや半径を計算してみると、他の第一原理的な計算と同様の結果が得られ、十分信頼できる方法であることがわかりました。また、酸素の同位体で計算してみたところ、他の方法で計算したときの結果と近い値が得られ、UMOAが中重核の領域においても信頼できる方法であることがわかりました。しかし、実験値とは合っておらず、核力に問題があることがわかりました(図3)。カルシウムやニッケルの同位体でも計算しましたが、同様の結果でした。
「UMOAは、多体計算の手法として十分信頼できるものだと思います。しかし、計算結果は、核子数が増大すると束縛エネルギーが増大し、荷電半径が小さくなる傾向がありました。ここから言えるのは、2体力だけでは原子核の飽和性は再現できないということ。また、物理量は原理的にはSRG変換のパラメータに依存すべきではないということから、少なくとも3体力効果を考慮する必要があることがはっきりと特定できました」。
もちろん多体系の核力を目標に計算を始めたのですが、この2体系による計算の結果で3体力の効果が必要なことがはっきりと示されました。「これからは3体力効果を取り入れて計算をしたい」と宮城さん。3体力を扱うのは容易ではありません。そのため、計算方法に一層の工夫が必要です。すでにテスト計算を始めていますが、多体系を扱うには計算手法を開発するだけでなく、「核力」についての新たな知見や大規模な計算資源が必要です。

図3：酸素同位体の基底状態エネルギー
計算結果がSRGパラメータに依存することから、少なくとも３体力が必要であることがわかる。

やってみるとおもしろい

数値計算で実験値を再現し、どこまで近づけるのか。宮城さんの挑戦は続きます。「この計算もたとえば10年前だったら実現しなかったでしょう」と宮城さんは言います。高速化など計算機の進化により、原子核の計算ができる範囲が広がっています。
「原子核の研究は非常に難しくて、研究のおもしろさに気が付くのには時間がかかりました。でもスパコンなど計算機の能力があがればあがるほど研究しやすくなりますから、原子核や素粒子などの研究はどんどんおもしろくなっていくでしょうね。これから研究を始めようとする若い人にもぜひとも取り組んでほしいと思います」。
現在は現象論的核力からスタートしていますが、将来はQCDの第一原理計算により得られた核力に基づいて原子核を解き明かしたいと、宮城さんは意欲的に研究を進めています。