原子核が球から楕円体に変形する-スーパーコンピュータ「京」で理論的に明らかに
計算基礎科学連携拠点
2017年8月3日
ポスト「京」重点課題9「宇宙の基本法則と進化の解明」サブ課題B原子核グループは、米論文誌『Physical Review Letters』に2016年10月から立て続けに、原子核の変形に関する論文を発表。その内4本がエディターズ・サジェスチョンに選ばれ、物理学上の重要な成果としてPRL誌に認められました。
本研究は、文部科学省HPCI戦略プログラム分野5「物質と宇宙の起源と構造」、ポスト「京」重点課題9「宇宙の基本法則と進化の解明」、および計算基礎科学連携拠点(JICFuS)のもとで、理化学研究所のスーパーコンピュータ「京」などを利用して得られたものです(課題番号:hp150224、hp160211)。
1.背景
原子核というと簡単には球形が想像されます。しかし、実はラグビーボール型やミカン型といった楕円体になることが多く、これを原子核の変形といいます。実験においては多くの核種で観測されています。ところが、どのような物理プロセスで、どのような形への変形が起こるのか、理論的な解明がまだ十分にはなされていません。実験で観測されていない不安定核ではなおさら理解が進んでいません。
2.成果(理論計算)
理化学研究所(理研)仁科加速器研究センターの大塚孝治・客員主管研究員、東京大学大学院理学系研究科の清水則孝特任准教授、富樫智章特任助教、角田佑介特任研究員らの研究グループは、ジルコニウム(Zr:原子番号40)に注目。モンテカルロ殻模型(MCSM)という独自の計算手法を用い、スーパーコンピュータ「京」で大規模な理論計算を実施しました。90Zrから110Zrまで2個刻みで原子核の状態を計算した結果、98Zrと100Zrの間で、球形から楕円体へと急激に変形する、量子相転移ともいえる現象が起こることを理論的に示すことができました(図1)。同時に、変形度も示しました。
水から氷に変化することを相転移といいます。相転移は通常、アボガドロ数のようなマクロな粒子が集まった系で起こる現象です。原子核は陽子や中性子がせいぜい100個程度しかありませんが、量子的な相転移が起こるかどうかが未解決の問題でした。それを今回、理論計算により明らかにしました。
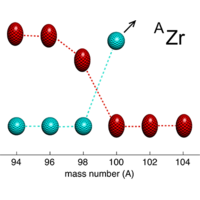
図1:ジルコニウム原子核の変形
98Zrより軽い原子核は球形(青)のエネルギーが低く安定している。100Zrより重い原子核は楕円体(赤)のエネルギーが低く安定する。98Zrと100Zrの間で球形から楕円体へと急激に変形が起こっている。(論文※1のエディターズ・サジェスチョンより転載)
2番目の論文の実験は、96Zrに対して独ダルムシュタット工科大学の研究グループが実施し、相転移直前の状況を明らかにしました。98Zrより重いZr核は自然界に存在しないため、理研RIBFのような特殊な実験装置が必要になります。すでに得られていた実験データがこの計算で初めて系統的に説明され、実験で知られていた98Zrから100Zrへの大きな変化が量子相転移として理論により初めて裏付けされました。
2017年1月の論文※3は、上記の理論論文の発展です。2016年10月の理論の論文の出版当時、110Zrの実験データは観測されていたものの未公開でした。実験グループから依頼があって共同研究を行い、観測と理論計算が一致することがわかりました。その驚異的な一致に誰もが驚きました。
2017年4月の論文※4は、角田特任研究員が中心に計算を行い、イタリア・ミラノ大学との共同研究の成果です。ここで注目したのはニッケル(Ni:原子番号28)です。66Niで、異なる形の量子状態が近いエネルギーで出現する変形共存現象が起きていることを示しました。それは「変形」の物理の一側面であり、極めて長寿命の励起状態(アイソマー)を生み出すこともわかりました。
3.成果(コード開発、可視化)
一連の研究成果の創出には、原子核の物理だけでなく、計算コードの開発と、計算結果の可視化が欠かせませんでした。
計算コードは、スパコンに計算させるための命令文です。モンテカルロ殻模型(MCSM)コードは2000年頃に、大塚客員主管研究員のほか、水崎高浩氏(現 専修大)、本間道雄氏(現 会津大)によって開発されました。モンテカルロではない普通の殻模型計算は古くからあり、現在も各国の研究グループが使用しています。殻模型計算には膨大な計算量が必要で、何の手段も講じなければ、世界中のスパコンを集めても限られた原子核に対してしか計算ができません。そこで全く異なる方法で計算を行う必要がありました。特に、原子核の変形に関しては、旧来の方法では満足のいく結果は得られていませんでした。
モンテカルロ法は、計算対象からランダムに取り出して計算を行い、結果を評価して確からしいものを積み上げていく統計的手法です。MCSMでは、それに対角化や変分といった計算上の要素も組み合わせます。計算コードは2000年頃に開発できていましたが、2010年頃、次世代スーパーコンピュータのプロジェクトが始まることを受けて、清水特任准教授を中心にコードを一から書き直しました。スーパーコンピュータ「京」が最大限の力を発揮できるように開発を行い、骨格が2012年にできあがって「京」を使った計算を開始。2013年にはコードが完成しました。2万行にも及ぶ大作です。以来、今日に至るまでマイナーチェンジはありましたが、同じコードで計算し続け、多くの成果が生み出されています。
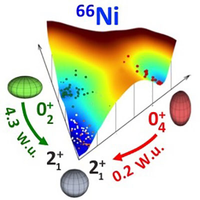
図2:66NiのTプロット表示
x軸(左右)とy軸(前後)は変形度を表し、右や後ろへいくほどつぶれた形となる。z軸(上下)はエネルギーで、赤が高く不安定、青が低く安定となる。MCSM計算による結果が丸で表示されており、エネルギーの低い青い部分にたしかに存在している。中央の一番低いところが球形(灰色)、右がラグビーボール型(赤)、左がミカン型(緑)である。(論文※4のエディターズ・サジェスチョンより転載)
スパコンによる計算結果は数字の羅列にすぎません。解析して初めて物理の探求が可能になります。そのため、一目でわかる結果、すなわち可視化が重要になります。角田特任研究員は、Tプロットという手法を考案し、エネルギーと原子核の変形との関係を可視化しました(図2)。物理的にも感覚的にもわかりやすいTプロットの導入もあり、MCSM計算は実験研究者からの問い合わせや共同研究の申し出が途切れることなく続いています。
4.今後の展望
今後は他の原子核種にも研究対象を広げつつ、個々の計算精度をあげていき、原子核の理解を進めます。
これまでの研究では、数値計算以外にも、殻進化、量子相転移、量子自己組織化のような新しいメカニズムや概念が生まれてきました。その中で、原子核の構造解明、特に不安定原子核の構造では、例えば、新しい魔法数34の理論的予言など多くの理論的貢献がありました。今回の一連の論文では、第2種殻進化※5が共通の基本メカニズムであることが示されています。
これからも、モンテカルロ殻模型のアルゴリズムの計算科学上の進歩、量子多体系の基礎物理的な発展、スパコンを使ったより高度な並列計算を3本の柱に、大規模な装置を使っての先端的な実験と組み合わせて、原子核の未知な世界への探究が続くでしょう。
脚注
※1
Quantum Phase Transition in the Shape of Zr isotopes, Tomoaki Togashi, Yusuke Tsunoda, Takaharu Otsuka, and Noritaka Shimizu, Phys. Rev. Lett. 117, 172502 – Published 17 October 2016
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.117.172502
※2
First Measurement of Collectivity of Coexisting Shapes Based on Type II Shell Evolution: The Case of 96Zr, C. Kremer, S. Aslanidou, S. Bassauer, M. Hilcker, A. Krugmann, P. von Neumann-Cosel, T. Otsuka, N. Pietralla, V. Yu. Ponomarev, N. Shimizu, M. Singer, G. Steinhilber, T. Togashi, Y. Tsunoda, V. Werner, and M. Zweidinger, Phys. Rev. Lett. 117, 172503 – Published 17 October 2016
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.117.172503
※3
Are There Signatures of Harmonic Oscillator Shells Far from Stability? First Spectroscopy of 110Zr, N. Paul et al., Phys. Rev. Lett. 118, 032501 – Published 18 January 2017
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.118.032501
※4
Multifaceted Quadruplet of Low-Lying Spin-Zero States in 66Ni: Emergence of Shape Isomerism in Light Nuclei, S. Leoni et al., Phys. Rev. Lett. 118, 162502 – Published 20 April 2017
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.118.162502
※5
The role of shell evolution in shape coexistence, T. Otsuka and Y. Tsunoda, J. Phys. G: 43, 024009 – Published 14 January 2016
doi:10.1088/0954-3899/43/2/024009
http://iopscience.iop.org/article/10.1088/0954-3899/43/2/024009/meta
お問合せ
本件に関するお問合せは計算基礎科学連携拠点広報室までお願いします。
お問合せフォーム














































