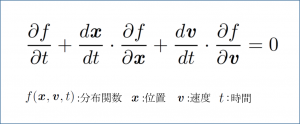ニュートリノや宇宙プラズマのシミュレーション精度が飛躍的に向上
-ブラソフ方程式の高精度数値解法を開発
国立大学法人 筑波大学
国立研究開発法人 海洋研究開発機構
国立大学法人 東京大学大学院理学系研究科/
国際高等研究所カブリ数物連携宇宙研究機構
2017年11月13日
研究成果のポイント
1.宇宙に広がる様々な粒子の運動を記述する重要な方程式であるブラソフ方程式の高精度数値解法を開発しました。
2.これまで、3次元空間では実行不可能とされていたシミュレーションの精度の飛躍的な向上につながります。
成果の概要
筑波大学計算科学研究センター 田中 賢研究員、吉川耕司講師、海洋研究開発機構 簑島 敬研究員、東京大学大学院理学系研究科/国際高等研究所カブリ数物連携宇宙研究機構 吉田直紀教授らは、ニュートリノや宇宙プラズマの運動を記述する基礎方程式「ブラソフ方程式」の高精度数値解法を開発しました。
ブラソフ方程式は、宇宙に広がる様々な粒子の運動を記述する重要な方程式です。ところが、ブラソフ方程式を用いたコンピュータ・シミュレーションには莫大なメモリ量が必要で、3次元空間での実行は不可能と考えられてきました。今回、高精度数値解法を開発したことにより、現実的なメモリ量でシミュレーションの精度を飛躍的に向上させることができます。
この研究成果は、2017年11月10日発行の天文学論文誌「The Astrophysical Journal」に掲載されました。
本研究は、文部科学省ポスト「京」重点課題9「宇宙の基本法則と進化の解明」、 および計算基礎科学連携拠点(JICFuS)の元で、 理化学研究所のスーパーコンピュータ「京」(課題番号:hp160212、hp170231)及びHPCIシステム利用研究課題で最先端共同HPC基盤施設のOakforest-PACS(課題番号:hp170123)を利用して得られたものです。
研究の背景
宇宙のほとんどの質量を担うダークマターやニュートリノ、惑星間や銀河間の空間に広がる希薄な宇宙プラズマ粒子の運動は、「ブラソフ方程式(無衝突ボルツマン方程式)」(図1)と呼ばれる共通の方程式に従います。ブラソフ方程式は素粒子やプラズマ粒子などの集団的な運動を記述するものです。この方程式を解くことで、粒子の数密度を位置や速度で表す分布関数(注1)が、時間と共にどのように変化するのかを厳密に求めることができます。
ダークマターや宇宙プラズマの運動の計算には、粒子シミュレーションが使われてきました。超粒子(注2)で物質分布を表現し、超粒子に働く力(ダークマターの場合は重力、プラズマ粒子の場合は電磁気力)を基に、個々の超粒子の運動を計算する方法です。しかし、粒子シミュレーションでは物質の連続的で滑らかな分布を超粒子の分布で表現するために、計算結果にノイズが入ってしまうという欠点がありました。
このノイズは、たとえば、宇宙空間を高速で運動するニュートリノがダークマターによる天体形成を遅らせる効果を計算する場合や、宇宙プラズマにおける磁気回転不安定性の成長を負う際には深刻な影響を及ぼすため、粒子シミュレーションではなく、物質の分布関数を連続体として扱うブラソフ方程式を用いて数値シミュレーションする必要があります。
ブラソフ方程式の解を解析的に求めることは非常に限られた場合以外は不可能で、実際には数値シミュレーションが不可欠です。分布関数は空間の3次元座標と3次元速度に依存するため、数値シミュレーションのためには「位相空間」(注3)と呼ばれる6次元の数学的な仮想空間の情報をコンピュータのメモリに記憶させる必要があります。しかし、6次元という高い次元を持つため、ブラソフ方程式の数値シミュレーションに必要なメモリ量は極めて多くなります。
一般的に数値シミュレーションを行う場合、小さな計算領域(メッシュ)に分割して方程式を解きます。たとえば四角い計算領域を考えて各辺をN個に分割すると、通常の3次元空間での数値シミュレーションではNの3乗に比例するメモリ量が必要ですが、ブラソフ方程式の数値シミュレーションではこれがNの6乗に比例してしまいます。分割数が大きければ大きいほど数値シミュレーションの精度は良くなるのですが、コンピュータで使えるメモリ量は有限であるため、「必要なメモリ量が極めて大きい」ブラソフ方程式の数値シミュレーションは精度の面で不利となります。この弱点を克服するために、ブラソフ方程式の解法をより高精度にする必要があります。
研究内容と成果
筑波大学計算科学研究センターの田中 賢研究員らの研究グループは、五次以上という高い精度をもつブラソフ方程式の数値解法を開発しました。この数値解法の特徴は、原理的には任意の精度をもつ数値解法を構築できることです。この数値解法によって、同じメモリ量のブラソフ方程式の数値シミュレーションでも格段に精度の良いシミュレーション結果を得ることが可能になりました。
図2は、一様な密度をもつ物質に密度の揺らぎをわずかに与えたときに、重力によって密度揺らぎが大きくなる様子をブラソフ方程式の数値シミュレーションで計算したものです。位置と速度の2次元の位相空間での物質“密度”を表し、赤色から白色にかけて密度が高くなっています。三次精度(注4)の結果では時間の経過とともに渦巻き状の構造がぼやけてしまうのと比較して、五次精度と七次精度の結果では細かい構造まで計算できていることがわかります。高精度な数値解法を用いることで、同じメッシュ数を使った数値シミュレーションでも結果が大きく改善されています。
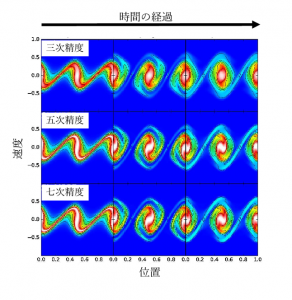
図2:一様な密度をもつ物質が自身の重力で収縮する様子
ブラソフ方程式の数値シミュレーションを用いて計算した。位置と速度の2次元の位相空間における物質密度を表している。1段目が三次精度の数値解法を用いた場合の結果で、2段目、3段目はそれぞれ五次精度、七次精度の数値解法を用いた場合の結果。
また、図3は図2の計算結果の物質密度を示したものです。三次精度で128メッシュを使って計算した結果は、同じく三次精度で1024メッシュを用いた結果と比べて大きく密度がなめされているのに対し、五次精度や七次精度で128メッシュを使って計算した結果は、1024メッシュを用いた結果とほぼ等しくなっており、この数値解法の精度の良さを示しています。
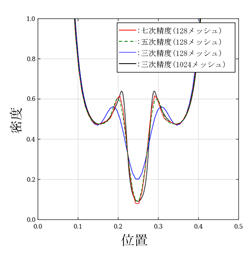
図3:図2の物質密度を示したもの
赤線は七次精度の数値解法を用いた128メッシュの場合の結果。緑線は五次精度の数値解法を用いた128メッシュの場合の結果。青線は三次精度の数値解法を用いた128メッシュの場合の結果。黒線は三次精度の数値解法を用いた1024メッシュの場合の結果。
この数値解法は、宇宙プラズマにおけるプラズマ粒子の数値シミュレーションでも精度の良い計算結果を与えることがわかりました。宇宙プラズマ中には磁場が存在しており、プラズマ粒子は磁力線の周りを回転運動するため、速度空間上では物質分布は旋回運動します。これまでのブラソフ方程式による数値シミュレーションでは、プラズマ粒子が速度空間上で旋回運動する様子を正確に計算することが困難でした。
図4は、プラズマ粒子の運動と同じ速度空間での旋回運動の、ブラソフ方程式による数値シミュレーションを行った結果です。色は物質の速度空間での密度を表しています。初期条件の分布を三次精度と七次精度の数値解法を用いて数値シミュレーションすると、右側2つの図のようになります。三次精度の数値解法では初期の密度分布が大きく変形して輪郭がぼやけているのに対し、七次精度の場合は初期の密度分布をほぼそのまま保っていることがわかります。
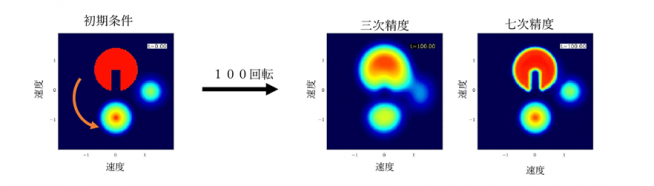
図4:速度空間での旋回運動をブラソフ方程式の数値シミュレーションで計算した結果
初期条件(左)での物質分布を図の中心の周りに100回転させたのが右の図。三次精度の数値シミュレーションでは初期条件の物質分布が崩れてしまうのに対し、七次精度では物質分布の境界以外ではほぼ変化せずに回転している。
このように、本研究で開発されたブラソフ方程式の数値解法は、これまでのものと比較して、シミュレーション結果の精度が飛躍的に向上しました。これまでは非現実的と思われるほどのメモリ量を使ってメッシュ数を増やさないと達成できないと思われていた計算精度が、現実的なメモリ使用量で達成できるようになりました。
今回の研究成果において、吉川講師は数値解法の設計・実装を、簑島研究員は数値解法の設計、田中研究員は設計した数値解法の高速化とテストを、吉田教授はテスト結果の検討を主に行いました。
今後の展開
本研究で開発したブラソフ方程式の高精度数値解法は、これまでのものと比べて精度が飛躍的に向上しています。これは、同じコンピュータを用いても格段に精度が高く、より正確なシミュレーション結果が得られることを意味しています。
今後の研究では、この数値解法を用いることで、粒子シミュレーションでは解明が困難な、宇宙大規模構造の形成過程におけるニュートリノの影響や宇宙プラズマの振る舞いに関する研究に取り組んでいきます。
用語解説
注1)分布関数
複数の粒子の運動は、位相空間では複数の点の集まりとして表される。ところが、宇宙空間のニュートリノやプラズマ粒子などの非常に多数の粒子の運動を表す場合は、位相空間上の数密度の形で表すのが便利であり、この数密度のことを分布関数と呼ぶ。
注2)超粒子
スーパーコンピュータで数値シミュレーションを行うときに、実際の素粒子やプラズマ粒子の集団をまとめて一つの仮想的な粒子と見なして扱う。その仮想粒子のことを超粒子と呼ぶ。
注3)位相空間
物質の運動状態を表す位置(3次元)と速度(3次元)からなる仮想空間。個々の粒子の運動は位相空間上の一つの点として表される。
注4)三次精度
メッシュの数を2倍にしたときに誤差の大きさが1/23倍(8分の1倍)になることを言う。五次精度なら32分の1、七次精度なら128分の1と、格段に精度が向上する。
掲載論文
【題 名】Multidimensional Vlasov–Poisson Simulations with High-order Monotonicity-and Positivity-preserving Schemes
(和訳:多次元ブラソフ方程式の高次精度数値解法)
【著者名】田中 賢(筑波大学計算科学研究センター)、吉川 耕司(筑波大学計算科学研究センター)、簑島 敬(海洋研究開発機構)、吉田 直紀(東京大学大学院理学系研究科/国際高等研究所カブリ数物連携宇宙研究機構)
【掲載誌】The Astrophysical Journal
DOI:10.3847/1538-4357/aa901f
問合わせ先
吉川 耕司(よしかわ こうじ)
筑波大学計算科学研究センター 講師
〒305-8572 茨城県つくば市天王台1-1-1
E-mail: kohji [at] ccs.tsukuba.ac.jp([at]を@に変えてください)