「富岳」による「格子QCDプログラム」が始動
現在、スーパーコンピュータ「京」に代わり、「富岳」の稼働に向けて着々と準備が進められています。「重点課題9」の中で、富士通と理化学研究所が共同で研究を進めている「富岳」を使った「格子QCDプログラム」の開発の取りまとめ役を担っているのが、広島大学の石川健一さんです。
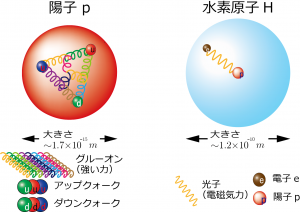
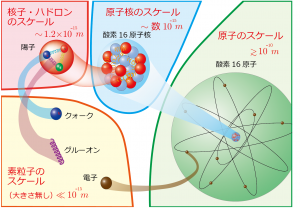
原子の性質は、電磁気学と量子力学を使って説明することができます。例えば、水素原子はプラスの電荷をもつ陽子とマイナスの電荷をもつ電子が互いに引き合って安定して存在している状態です(図 1右)。様々な原子(元素)は、正の電荷を帯びた原子核の周りをいくつかの電子が取り巻くことで、安定な状態になっています。この宇宙には様々な元素がありますが、元素ごとに原子核の種類があります。原子核の持つ正の電荷量が、その元素の化学的性質を決めています。実はこの様々な原子核は、陽子と中性子の集合体で、陽子と中性子の間には核力が働いています。この核力は、電磁気よりもとても強い力で、原子核の中に正の電荷を持つ陽子を複数保持して安定させることができます。現代の素粒子論では、陽子や中性子はさらに3種類のクォークでできており、クォークとクォークの間にはグルーオンが存在することまでわかっています(図 1左と図 2)。クォークとグルーオンの量子力学に対応するものが「量子色力学(QCD)」と呼ばれている理論です。
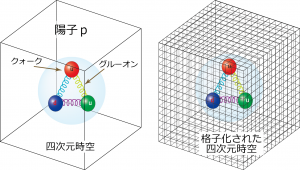
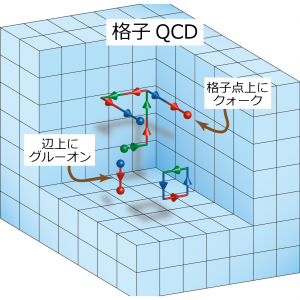
陽子や中性子がクォークとグルーオンで構成されていることはわかっているのですが、具体的に、陽子や中性子の質量を簡単かつ定量的に、クォークとグルーオンのQCDで説明することはできていません。しかし、スーパーコンピュータを用いて大量の計算を行うことで、説明できるようになってきました。このQCDを、スーパーコンピュータを用いて解く方法として、「格子量子色力学」、すなわち「格子QCD」という理論が使われています。格子QCD理論では、4次元の時空を正方形の格子状に切っていき(図 3)、それぞれの格子点に、クォークを定義し、さらに、格子点と格子点を結ぶ線に、クォーク同士を結びつけるグルーオンを定義しています(図 4)。それにより、コンピュータ上で、現実的な時間内に、計算を終了することができるようになっています。「格子QCDプログラム」は、この4次元格子上のクォークやグルーオンのQCDの計算を行うためのプログラムです。
QCDは、電子と電磁場の理論である電磁気学ととても似ています。電磁場の運動方程式はマックスウェル方程式を、電子の運動方程式はディラック方程式を使って、それぞれ記述します。特に、電磁気学をミクロの世界まで適用できるように量子力学と統合したものを、「量子電気力学(QED)」といいます(図 5)。
この理論は、素粒子理論で大変成功しています。この成功の背景には、電磁気力のちからの大きさが比較的弱いことがあります。QEDでの理論計算では、この電磁気力が弱いことを利用した解析的な近似計算が大変良い近似になっています。実験値との比較が系統的に正確にできるからです。ミクロな世界での電磁気現象に関わる実験値を、QEDによる精度の良い理論計算を用いて、よく説明することができました。
しかし、QCDはQEDと大変似ているものの、陽子の真の性質を、クォークやグルーオンの力学であるQCDを用いて理解するには、QCDの力が強いため、QEDで大きな成功を収めた解析的近似手法を使うことができませんでした。
QCDと電磁気学の違いは大雑把に言うと、電磁気学の電場や磁場は電気を帯びておらず、中性であるのに対して、QCDにおける電場や磁場に対応する力の場は、電荷に対応する色電荷もしくは色荷というものを帯びている点です(図 1と図 5)。クォークもこの色荷を持っています。これは、電子が電荷を持つことに対応します。
QCDにおける電場や磁場が色荷を持つため、方程式は電磁気のマクスウェル方程式に似ていますが、すこし違うところがあります。このため、QCDの力は、遠方になるにしたがって、雪だるま式に強くなると考えられています。そこで、1974年に、アメリカの物理学者の故・ケネス・G・ウィルソン博士(1936~2013、1982年にノーベル物理学賞受賞)によって開発されたのが、冒頭で紹介した格子QCDという手法でした。
陽子は、電磁気の電荷が1の単位量を持ちますが、その中には、クォークが3つ含まれていると、QCDは予言します。そうすると、クォークの電磁気力の電荷は1/3 を単位とする電荷を持つはずです。高エネルギーの電子陽子衝突実験などで陽子の中を調べると、確かにクォークが1/3の電荷単位を持って存在しているようです。
しかし、そのクォークを単独で取り出して、その1/3単位の電荷を測ることはできていません。クォークを単独で取り出すことができないという実験事実は、「クォークの閉じ込め」と呼ばれています。この実験事実をQCD理論から説明することはできませんでした。それは、QCDの力が大きいため、QEDで成功した解析的近似方法が使えないからです。そこで、ウィルソン博士が、このクォークの閉じ込め現象を理論的に説明するために編み出したのが、格子QCDだったのです。
具体的には、4次元の時空を格子状に切り、その格子上で、グルーオンのマックスウェル方程式と、クォークのディラック方程式を解いていきます。QCDにおけるクォークの色荷は3種類、グルーオンの色電磁場は8種類あります。8種類のグルーオンの色電磁場は、格子の辺上に定義します。また、格子の点上に定義されたクォークの運動によって、辺上にあるグルーオンが揺らぎ、波のように周囲に伝搬していきます(図 4)。運動方程式は全て、この格子の上に乗るように定義されているのです。
ウィルソン博士は最初、色荷が小さく、力が弱いと仮定した場合の近似計算と、色荷が大きく、力がとても大きいと仮定した場合の近似計算を解析的に行っていました。特に、力が大きい場合に、クォークの閉じ込めが起こることを確かめました。しかし、この場合、格子の近似が粗いため、現実世界の連続的な時空とみなすには問題がありました。
ところが、そのすぐ後の1980年に、アメリカの理論物理学マイケル・クロイツ博士が、小さな体積でクォークは含まず色は2種類だったものの、コンピュータを用いた近似なしの格子QCDの計算を行い、クォークの閉じ込めを定量的に説明することに成功しました。さらに、その後の長年に亘る理論的研究とスーパーコンピュータの発展により、今日、格子QCDの数値計算は、理論と実験に加えて第三の科学的手法として確立してきています。
『富岳』における格子QCDの課題と今後の目標
現在、格子QCDの計算には、「モンテカルロ法」と呼ばれる多重積分(重み付き積分)が使われています。また、格子QCDは量子力学を扱っているため、確率の世界になります。計算によって求めることができるクォークとグルーオンに関する物理量は期待値であり、平均値です。そのため、格子QCDでは、サイコロのようなものが定義されています。サイコロの形状は、その都度、運動方程式によって決まります。コンピュータ上で、サイコロを何度も何度も振り、出た目の値の平均値を最後に求めるという方法をとっています。「格子QCDのサイコロを振る」ということは、「クォークやグルーオンのふるまいのスナップショットを沢山作る」ということを意味しています。
そのため、一般的なサイコロは立方体で、6面しかありませんが、格子QCDのサイコロは、なんと無限の面を持ちます。その1つ1つの面が、ある時空上におけるクォークとグルーオンのふるまいのスナップショットになっているのです。
たとえば、サイコロの目の2乗の平均値を計算する場合、出た目の値をそれぞれ2乗して足し、サイコロを振った回数で割って、平均値を出しますよね。モンテカルロ法でも同様の操作を行っています。サイコロを1回振ることにより、クォークやグルーオンのスナップショットから物理量が1つ求められます。それを何回も繰り返していき、さらに、物理量の平均値を計算することで、その物理量を決定しています。
ここでの最大の課題は、サイコロをうまく作ることです。その方法も、格子QCDの研究者が編み出しました。「ハイブリッドモンテカルロ法」と呼ばれています。今では、素粒子物理だけでなく、経済の株の動きやAIなど多重積分が必要な場面では、このハイブリッドモンテカルロ法が多用されています。
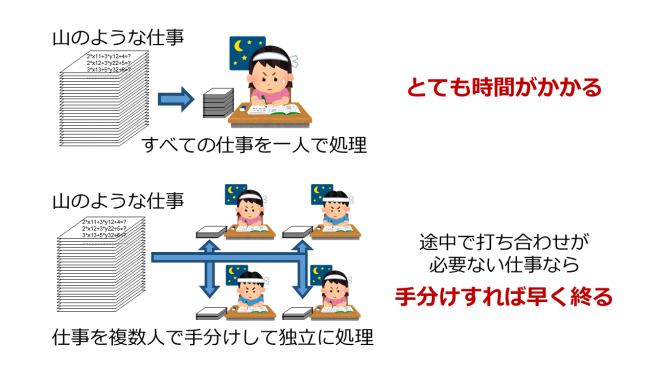
「また、スーパーコンピュータを使わなければ計算できない最大の理由は、クォークの運動方程式が、非常に大規模になるからです。格子の上に乗ったクォークの運動方程式は、とても大きな連立方程式になります。ハイブリッドモンテカルロ法では、このクォークの運動方程式に対応する連立方程式を何回も解く必要があります。例えば、4次元格子の大きさが 164程度の場合、連立方程式の大きさは約150万次元という非常に大きなものです。したがって、厳密にすべての未知数を求めることはできません。必要な精度で、近似的に解く必要があるのです。それでも計算量は膨大です。そのため、工夫が必要でした」と石川さんは話します(図 6)。
現在のところ、ハイブリッドモンテカルロ法では、統計誤差10%以下で物理量を決めるためには、1000~10000個のサンプル数が必要なことがわかっています。そのためには、たとえば、クォークの物理量を計算する場合、クォークの運動方程式を105~106回解かなければならないといいます。しかし、仮に、クォークの運動方程式を1回解くのに30秒ほどかかったとすると、1個の平均値を取得するのに、サンプル数が1000個の場合、35日以上、10000個の場合、350日以上かかる計算です。また、サンプル同士は、強い相関関係があるため、前の計算結果を基に次の方程式が決まり、その方程式に基づき、次の計算をしなければなりません。そのため、同時並行的に分散処理することができません。
「したがって、1回1回の計算を、いかに高速かつ効率良く実行するかが重要な課題です。しかし、そのための手段がないというのが現状です。格子QCDで扱う運動方程式は、構造が簡単なため、複雑な運動方程式を解く場合とは異なり、高速化のための工夫の余地がないのです。ハードウェアの性能に依存せざるを得ず、ハードウェアによって律速してしまう点が、大きな課題です」と石川さん。
通常、ハードウェアでは、メモリにあるデータをCPUに送信し、CPUで計算して計算結果を再度メモリに保存します。ここで、送受信するデータ量が膨大な場合、データを送受信できるメモリ容量によって、計算速度が左右されます。これを「メモリバンド幅によって律速される」といいます。メモリバンド幅とは、データを送るための道幅のことです。
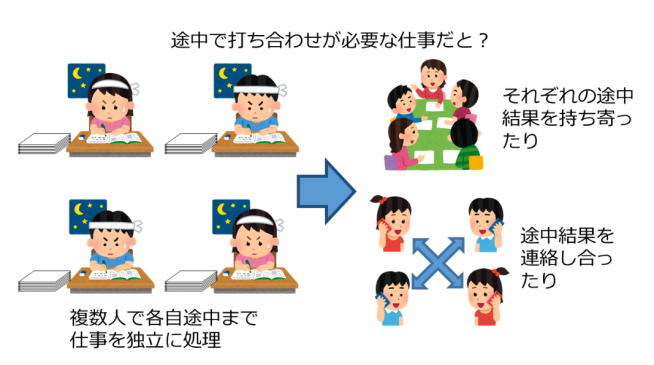
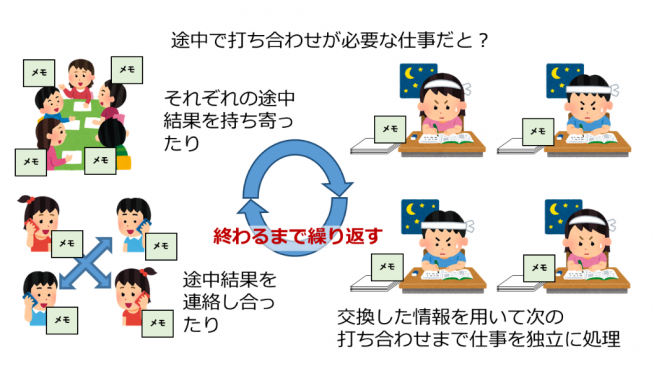
また、並列分散処理する場合には、並列処理要素の間でデータをやり取りするためのネットワーク性能も重要です。並列分散処理において、一つの問題を処理する際に、並列処理要素の間でのデータのやり取りが頻繁に必要となる場合、先のメモリバンド幅に加えて、ネットワーク性能によっても、全体の性能が作用されます(図 7と図 8)。
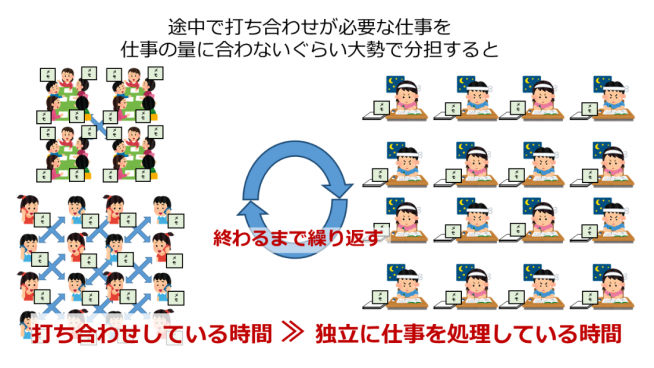
「現在のスーパーコンピュータに搭載されているCPUの性能は、パソコンに搭載されているものと、ほとんど変わりません。複数のCPUが手分けして、並列分散処理を行うことで、計算速度の高速化、高性能化を図っているのです。しかし、格子QCDの場合の分散並列処理は、4次元格子を分割して行っています。とくに、格子QCDの場合、クォークの運動方程式を解く問題が、並列処理要素の間のデータのやり取りが頻発する部類の問題になっているのです(図 8と図 9)。
4次元格子の大きさは固定して計算をしたいのですが、並列数を上げていくと、一つの処理単位に担当する4次元格子の大きさが、どんどん小さくなっていきます。そうすると、並列処理要素単位の性能が悪化するとともに、ネットワーク性能に律速されて、どんどん効率が悪くなっていきます。このため、並列度を高めても、計算処理速度が上がりません(図 10)。このことは、『富岳』やさらにその先のスーパーコンピュータにおける格子QCDの大きな課題です。そのため、『富岳』では、アルゴリズムの工夫が、研究の中心になっていくと考えています」と石川さんは話します。
一方で、「富岳」では新たに、「半精度」が使えるようになるため、石川さんはその点に期待をしています。半精度とは、数値計算を行う際の小数点の数の精度のことです。それにより、処理すべきデータ量が削減され、メモリバンド幅やネットワーク性能の問題が緩和されることが期待されます。
現在、最も一般的なのが「倍精度」で、十進数でおよそ15桁(64ビット)の有効数字を取り扱えるフォーマットです。「単精度」というフォーマットもあり、およそ7桁(32ビット)の有効数字を取り扱うことができます。しかし、近年、ディープラーニングなどの計算では、倍精度や単精度までは必要ないことがわかってきました。そこで、さらに精度を落としたおよそ3桁(16ビット)の有効数字を取り扱える半精度というフォーマットが出てきたのです。半精度は、単精度や倍精度に比べてデータサイズが小さいため、メモリバンド幅によって律速されにくいという特徴をもっています。
「倍精度で、1回連立方程式を解いた結果と、単精度で3回連立方程式を解いた結果が同じになること、加えて、データ量が少ないため、単精度で3回計算するのにかかる時間の方が、倍精度で1回計算するのにかかる時間に比べて短いことが、すでに確認されています。この性質が半精度でも成り立つことが期待されています。そこで、『富岳』では、半精度のフォーマットを使うことにより、計算処理速度の向上を図っていく計画です」と石川さん。
 最後に、今後の「富岳」でのプロジェクトの目標について石川さんはこう語ります。「『京』では、8年間の運用期間のうち、最初の3年間で、グルーオンの配位を算出し、3年目以降に、クォークの物理量の計算を行い、その結果を基に、後半の5年間で多くの論文を発表してきました。現在、『富岳』の稼働に向けては、『京』を使って得たクォークの物理量を基に、それぞれの研究者が、それぞれの目的に応じて、陽子の質量やバリオンの質量など、自分が求めたい物理量を求めるというフェーズに入っています。
最後に、今後の「富岳」でのプロジェクトの目標について石川さんはこう語ります。「『京』では、8年間の運用期間のうち、最初の3年間で、グルーオンの配位を算出し、3年目以降に、クォークの物理量の計算を行い、その結果を基に、後半の5年間で多くの論文を発表してきました。現在、『富岳』の稼働に向けては、『京』を使って得たクォークの物理量を基に、それぞれの研究者が、それぞれの目的に応じて、陽子の質量やバリオンの質量など、自分が求めたい物理量を求めるというフェーズに入っています。
一方で、格子QCD自体はすでに完成した理論ですので、精密化やアルゴリズムの工夫が今後の課題になります。格子QCDの格子間隔を縮め、より解像度を高めることや、格子の体積の大きさを自由に変えられようにすることに取り組んでいく計画です。クォークは現実世界では、電磁気の電荷を持っていますが、格子QCDと量子電気力学を一緒に計算する手法は、世界的にまだ始まったばかりです。実際、陽子は電荷が1、中性子は電荷が0で、質量がわずかに異なっています。そのため、『富岳』では、陽子と中性子の質量の違いを説明できるような、クォークの電荷とクォークの質量の違いを取り入れる計算手法の研究も進めていきます」