FOM 法のバックアップ(No.3) - JICFuS Wiki

[ トップ ] [ 新規 | 一覧 | 単語検索 | 最終更新 | ヘルプ ]

バックアップ一覧
差分を表示
現在との差分を表示
ソースを表示
FOM 法へ行く。
- 1 (2012-03-16 (金) 02:34:13)
- 2 (2012-03-16 (金) 02:36:55)
- 3 (2012-03-28 (水) 19:07:49)
- 4 (2012-03-30 (金) 02:24:27)

1 線形方程式の解法の選択
 2 参考文献および参考書の記述
線形方程式, 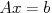>>> 実非対称/複素非エルミート, >>> 安定性重視 >>> FOM 法

概要
導出
アルゴリズム
- FOM法
- 前処理付きFOM法
サンプルプログラム
適用事例
参考文献および参考書
- 原著論文
- 教科書

概要 †

FOM法(完全直交化法)は1981年にSaadよって提案された非エルミート線形方程式向けのKrylov部分空間法である.

初期近似解を, 対応する初期残差をと置く. この時, GMRES法の反復目の近似解は,

のように, 初期近似解とクリロフ部分空間で張るアフィン空間に含まれ,

の直交条件(Ritz-Galerkin条件)を満たすように設定される.

Krylov部分空間の基底として, Arnoldi原理によって生成された正規直交基底を用いる. Arnoldi原理は長い漸化式を持つため, 反復回数の増加に伴って, 反復当たりの演算量および記憶容量が増大する. このため, 実用上はリスタート版のFOM(m) 法やトランケート版のDIOM(m)法が用いられる.

CG 法を非エルミート線形方程式へ拡張した解法であり, FOM法をエルミート線形方程式に対して適用した場合は, CG法と数学的に同値である.

導出 †

準備中

アルゴリズム †

FOM法 †

Set an initial guess
Compute
Set
For
　　
　　For
　　　　
　　　　
　　End For
　　
　　
　　For
　　　　
　　End For
　　If then
　　　　
　　　　
　　　　Stop
　　End If
　　
　　
　　
　　
　　
　　
End For

前処理付きFOM法 †

Set an initial guess
Compute
Set
For
　　
　　For
　　　　
　　　　
　　End For
　　
　　
　　For
　　　　
　　End For
　　If then
　　　　
　　　　
　　　　Stop
　　End If
　　
　　
　　
　　
　　
　　
End For

サンプルプログラム †

準備中

適用事例 †

準備中

参考文献および参考書 †

原著論文 †

[13] Yousef Saad, Krylov subspace methods for solving large unsymmetric linear systems, Mathematics of Computation 1981; 37(155):105–126.

教科書 †

[14] Yousef Saad, Iterative Methods for Sparse Linear Systems, 2nd ed., SIAM: Philadelphia, PA, 2003.
P159–161