1 線形方程式の解法の選択
2 参考文献および参考書の記述
線形方程式, 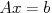>>> 実対称/複素エルミート, >>> 正定値 >>> CG 法

概要 †

↑

導出 †

↑

2次関数最小化としての導出 †

線形方程式の真の解をと置く. この時, 2次関数

 
 

は, を満たす. そこで, 2次関数の最小化問題

 
・・・(1)
 

を(反復法で)解くことで, 線形方程式の解を得ることを考える.

↑

逐次最小化法 †

最小化問題(1)を解く単純な反復法として, 適当な初期近似解に対し,

  1. 何らかの方法で, 探索方向ベクトルを定める.
  2. を最小化するようを設定し, のように解を更新する.

を繰り返すアルゴリズムが考えられる. このアルゴリズムは逐次最小化法とよばれ, 1次元最小化の係数はとして容易に計算出来る.

↑

最急降下法 †

探索方向ベクトルの設定によって様々な逐次最小化法が存在するが,

 
 

のようににおけるの最急降下方向に選ぶのが最も自然な方法であろう. この方法は最急降下法と呼ばる. 最急降下法は目的関数が単調に減少し, 直感的には優れた方法ではあるものの, 計算精度および収束性の面から実用的でないことが知られている.

↑

共役方向法 †

一方, 一般の逐次最小化法で得られる近似解はアフィン空間

 
 

に属する. ここで, 逐次最小化法(の探索方向ベクトル)に適当な修正を加えることで, アフィン空間上で目的関数の最小化をすることを考える. 証明は割愛するが, 探索方向ベクトルに対し,

 
・・・(2)
 

を仮定すると, 以下が成り立つ.

このように逐次最小化法の探索方向ベクトルに対し(2)の条件を課すことで改良した方法を共役方向法と呼ぶ.

↑

共役勾配法 †

最急降下法に基づく共役方向法として,

 
 
 

と設定する方法を共役勾配法(Conjugate Gradient法)と呼ぶ. また, CG法のはそれぞれ,

 
 

のように変形出来る.

↑

クリロフ部分空間法としての導出 †

初期近似解を, 対応する初期残差をと置く. また, Krylov部分空間

 
・・・(3)
 

の基底を列に持つ行列をと置く. この時, 一般に, Krylov部分空間法の反復目の近似解および対応する残差は,

 
 

と書ける. ここで, である. 基底の生成アルゴリズムおよびベクトルの設定法によって各種のKrylov部分空間法は導出される.

CG法は, Lanczos原理に基づき基底を, またベクトルはRitz-Galerkin条件に基づき設定される.

↑

Lanczos原理 †

行列がエルミート行列であることに注目すると, Krylov部分空間(3)の正規直交基底は, Gram-Schmidtの直交化に基づくLanczos原理により生成される. Lanczos原理のアルゴリズムは以下のように書かれる.

  1. Set
  2. For
  3. 　　
  4. 　　
  5. 　　
  6. 　　 If then Stop
  7. 　　
  8. End for

ここで, 行列を三重対角行列

 
 

と置くと, Lanczos原理の行列表現

 
・・・(4)
 

を得る. ここで, とする.

↑

Ritz-Galerkin条件 †

CG法のベクトルは残差ベクトルが

 
・・・(5)
 

の直交性を持つよう設定される. この直交条件をRitz-Galerkin条件と呼ぶ.

↑

CG法導出の基本原理 †

Lanczos原理の行列表現(4)およびRitz-Galerkin条件(5)より,

 
 

が成り立つ. ここで, である. 従って, ベクトルは次の線形方程式

 
・・・(6)
 

を解くことで計算される.

↑

導出の詳細 †

係数行列がHPD(正定値エルミート行列)である場合, 方程式(6)は常にCholesky分解により解くことが出来る. 方程式(6)をCholesky分解を用いて解く方法をLanczos法と呼び, LQ分解分解を用いて解く方法をSYMMLQ法と呼ぶ. SYMMLQ法は不定値な行列に対しても適用可能である.

一方, CG法の導出はLanczos法やSYMMLQ法と少し異なる. 行列をそれぞれ, を満たす正定値対角行列および単位上三角行列とする. また, およびと置く. この時, 近似解は

 
・・・(7)
 

と書ける.

式(7)およびの定義から, ベクトルは

 
 

の漸化式により計算出来る. ただし, とする.

一方で,

 
 

の関係式およびRitz-Galerkin条件(5)から, に対し,

 
 

が成り立つ. これらの条件が成り立つよう, 漸化式のは

 
 

のように設定される.

↑

アルゴリズム †

↑

CG法 †

  1. Set an initial guess
  2. Compute
  3. For
  4. 　　
  5. 　　
  6. 　　
  7. 　　
  8. 　　
  9. End For
↑

前処理付きCG法 †

  1. Set an initial guess
  2. Compute
  3. For
  4. 　　
  5. 　　
  6. 　　
  7. 　　
  8. 　　
  9. End For
↑

サンプルプログラム †

準備中

↑

適用事例 †

準備中

↑

参考文献および参考書 †

↑

原著論文 †

[10] Magnes R. Hestenes and Eduard Stiefel, Methods of conjugate gradients for solving linear systems, Journal of Research of the National Bureau of Standards 1952; 49(6):409–436.

↑

教科書 †

[2] Richard Barrett, Michael W. Berry, Tony F. Chan, James Demmel, June Donato, Jack Dongarra, Victor Eijkhout, Roldan Pozo, Charles Romine and Henk A. van der Vorst, Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, SIAM: Philadelphia, PA, 1993.
P14–17

[14] Yousef Saad, Iterative Methods for Sparse Linear Systems, 2nd ed., SIAM: Philadelphia, PA, 2003.
P187–194

[27] Henk A. van der Vorst, Iterative Krylov Methods for Large Linear Systems, Cambridge University Press: New York, NY, 2003.
P37–47

[23] Masaaki Sugihara and Kazuo Murota, Theoretical Numerical Linear Algebra, Iwanami Press: Tokyo, 2009, (in Japanese).
P148–153

[29] 藤野 清次, 張 紹良, 反復法の数理 (応用数値計算ライブラリ)　朝倉書店, 1996.
P31–35

トップ   新規 一覧 単語検索 最終更新   ヘルプ   最終更新のRSS