![[JICFuS Wiki] [JICFuS Wiki]](image/pukiwiki.png)
![[JICFuS Wiki] [JICFuS Wiki]](image/pukiwiki.png)
1 線形方程式の解法の選択
2 参考文献および参考書の記述
線形方程式, 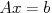 >>> 実対称/複素エルミート,
>>> 実対称/複素エルミート,  >>> 省メモリ型 >>> 最急降下法
>>> 省メモリ型 >>> 最急降下法
線形方程式 の真の解を
の真の解を と置く.
この時, 2次関数
と置く.
この時, 2次関数

は,  を満たす.
そこで, 2次関数
を満たす.
そこで, 2次関数 の最小化問題
の最小化問題
 ・・・(1)
・・・(1)を(反復法で)解くことで, 線形方程式 の解を得ることを考える.
の解を得ることを考える.
最小化問題(1)を解く単純な反復法として, 適当な初期近似解 に対し,
に対し,
 を定める.
を定める. を最小化するよう
を最小化するよう を設定し,
を設定し,  のように解を更新する.
のように解を更新する.を繰り返すアルゴリズムが考えられる.
このアルゴリズムは逐次最小化法とよばれ, 1次元最小化の係数 は
は として容易に計算出来る.
として容易に計算出来る.
探索方向ベクトル の設定によって様々な逐次最小化法が存在するが,
の設定によって様々な逐次最小化法が存在するが,

のように における
における の最急降下方向に選ぶのが最も自然な方法であろう.
この方法は最急降下法と呼ばる.
最急降下法は目的関数
の最急降下方向に選ぶのが最も自然な方法であろう.
この方法は最急降下法と呼ばる.
最急降下法は目的関数 が単調に減少し, 直感的には優れた方法ではあるものの, 計算精度および収束性の面から実用的でないことが知られている.
が単調に減少し, 直感的には優れた方法ではあるものの, 計算精度および収束性の面から実用的でないことが知られている.
ただし,CG 法で保存されるベクトルが の計5本であるのに対し,最急降下法では
の計5本であるのに対し,最急降下法では の4本と少ない.
(ここで,$math(\vec{b};は場合によっては不要である.)
の4本と少ない.
(ここで,$math(\vec{b};は場合によっては不要である.)












準備中
準備中