核変換とは、原子核を別種の原子核に変えることです。核変換には放射性廃棄物処理を始めとして、様々な応用が考えられますが、核変換をどのような方法で実現できるかは研究途上です。
核変換とは、原子核を別種の原子核に変えることです。核変換には放射性廃棄物処理を始めとして、様々な応用が考えられますが、核変換をどのような方法で実現できるかは研究途上です。
研究を進めるには、まず核変換を起こす反応を理解することが重要で、そのためには反応前後の原子核の量子状態を明らかにする必要があります。東京大学大学院理学系研究科特任助教の富樫智章さんは、モンテカルロ殻模型という方法によって、まだだれもやったことのない、核変換前後の原子核の量子構造を大規模シミュレーションで解明する研究に挑んでいます。
注目される核変換反応
陽子と中性子(あわせて核子という)からなる原子核は、核子の間にはたらく核力によって一つの塊になっていますが、内部の構造や性質には不明な点が多く、さまざまな研究が進められています。中でも注目されているのは核変換反応です。
原子炉で核分裂反応を行うと、人工的な核種が生じます。その中には、半減期(寿命)が数十万~数百万年と非常に長いものがあり、長寿命核分裂生成物と呼ばれています。これは、数十万~数百万年ものあいだ放射線を出し続ける危険な核種であることを意味します。もし、長寿命核分裂生成物を核変換反応によって寿命の短い核種に変えることできれば、高レベル放射性廃棄物の低減化や資源化につながる可能性があります。そこで今、核変換反応の実現に向けた議論が盛んに行われ、そのための基礎研究が始められました。
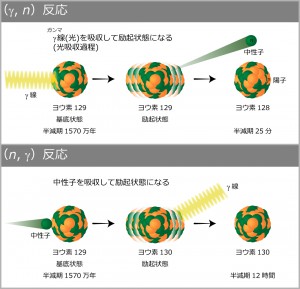
核変換反応には、2つの方法があります。ひとつは、γ線(光)を長寿命原子核に当てて不安定な状態にすることです。γ線によって与えられたエネルギーがあるレベルを超えると、不安定な原子核は中性子を放出し、安定な別の原子核になります。この反応を(γ,n)反応といいます。もうひとつは、(n,γ)反応といい、原子核に中性子を吸収させて別の原子核にする方法です。原子核が中性子を吸収すると不安定な状態になり、安定な状態に戻るときに光を出します。
ヨウ素129の半減期は1570万年ですが、γ線を当てる(γ,n)反応の結果、半減期が25分のヨウ素128になり、中性子を吸収させる(n,γ)反応では、半減期が12時間のヨウ素130になります(図1)。このような(n,γ)反応や(γ,n)反応は、恒星の内部などで元素が合成される過程で起こると考えられています。
光を吸収する(γ,n)反応
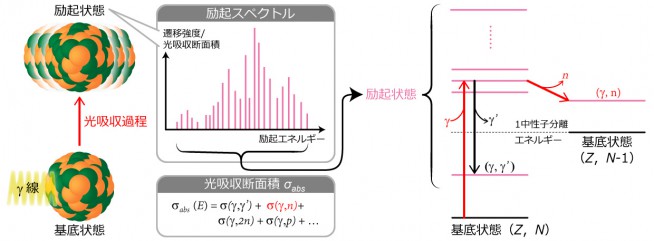
原子核に光を当てる(γ,n)反応では、原子核が光を吸収する過程で、不安定な励起状態(安定な基底状態よりエネルギーが高い状態)に移行します。そのとき得られた励起スペクトルから、この励起が起こる原因や、どのエネルギーでどれだけの反応が起こるかがわかります(図2)。
「この励起スペクトルは、原子核の構造に依存しています。原子核の構造を見る点でも励起スペクトルはとても興味深いものです」と富樫さんは話します。
また、励起スペクトルから、光吸収断面積が求められます。光吸収断面積とは、どのエネルギーでどれだけの反応が起こるか、つまり反応の起こりやすさを示しています。この光吸収断面積は、原子核における核変換反応の起こりやすさの尺度となる重要なデータです。
不可能な計算を可能にするモンテカルロ殻模型
そこで、富樫さんは理論計算によって、長寿命核分裂生成物が光を吸収して励起する過程を記述するとともに、光吸収断面積を求めようとしています。「励起エネルギーはシュレディンガー方程式を解けばわかるのですが、そのときの原子核の量子状態を計算するには、殻模型計算を使うのが有効です」と富樫さんは話します。
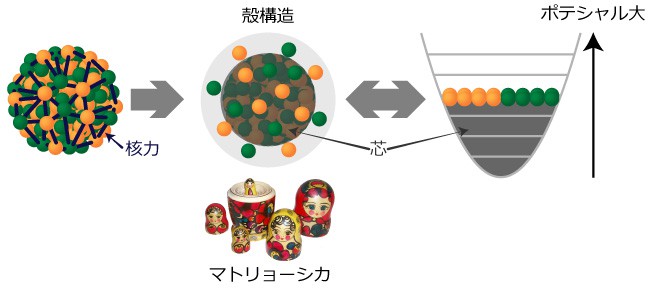
図3:殻模型
原子核は核子どうしが核力により全体を形作っている。核力の性質は複雑だが、原子核は殻の構造の中に核子を詰めていったものとする殻模型を使うと、原子核の多くの性質が理解できる。殻構造を核子全体がつくるポテンシャルのくぼみの中に核子が閉じ込められた状況として、殻構造を計算するのが殻模型計算。
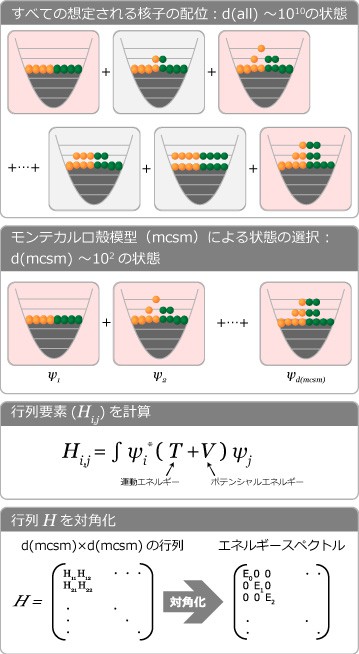
図4:モンテカルロ殻模型
殻模型において想定される核子すべての状態から、モンテカルロ法の考えを利用して選び出す。選び出された状態を使って行列の要素を計算し、さらに対角化という行列特有の操作を行う。そのほか、核力などさまざまな要因を加えて行列要素を計算すると、莫大な計算量になるが、エネルギースペクトルや原子核の形状など多くのことを調べることができる。
モンテカルロ殻模型(からもけい)とは、原子核の構造を記述するモデルのひとつです。原子核は中性子と陽子が互いに核力を及ぼしあって、全体を形作っています。原子核の中では、陽子や中性子はある軌道を回っており、その起動はマトリョーシカのように入れ子になって、中心から殻を作っているというのが、殻模型です。このモデルを使うと、原子核は殻の中に陽子や中性子をつめたものと理解できます(図3)。
原子核の安定性は、陽子、中性子の数と深く関わっており、原子核を安定にさせる特定の数(魔法数)が存在すると考えられています。そこで、殻模型計算では、陽子数または中性子数が特定のであるときに殻が閉じて安定化するという殻構造を仮定したうえで、相互作用する陽子や中性子の運動を計算します。
実際に殻模型計算を行うときは、軌道上の中性子や陽子の配置、つまり殻の中に陽子や中性子をどう詰めていくかという配置をすべての組み合わせについて考えます。すると、質量が100を超えるような大きな原子核を扱う場合、使う状態の数は1010を超え、計算量は爆発的に増えてしまうので、いくらスパコンを使っても計算することは不可能です。
そこで、確率的なモンテカルロ法を用いて、計算に必要な配置の組み合わせを選び出します。そうすれば、1010あった状態の数が100~1000に抑えられます(図4)。
「ふつうならあきらめる計算を、物理的に必要な範囲を選び出すことによって計算が可能になります」と富樫さん。それでも計算量は多いので、スーパーコンピューター「京」を使わないと計算できません。そのための、ノウハウも必要です。「実際に計算するには、核子の運動エネルギーや核子の相互作用によるエネルギーを計算しなくてはなりません。核力などの期待値を計算するのが大変でした」。
教科書を書き換えるような研究をめざす
富樫さんがまず行ったのは、実験から求めた既存のデータを計算で再現し、新たに始めた計算法の妥当性を確認することです。「計算には核子どうしの相互作用がとても重要です。また、実験値を再現するためには、なるべく実験値に近づくように計算のパラメータを調整しなければなりません。核子がどの軌道にあったときにどういう相互作用があるかを考えながらパラメータを決めます。決めるまでは試行錯誤が続き、何度も計算を繰り返さなければならないのでとても時間がかかります」。
富樫さんの行う計算は、「京」1000ノード(全体の1%強)を使って1日かかります。同じ計算を大学などにあるスパコンを使えば10日はかかります。これを何度も繰り返すのですから、かなり大規模な計算であることがわかります。
現在、富樫さんが計算しているのはストロンチウムの原子核です。実験データを前提にストロンチウム88を計算し、ほぼ実験を再現するデータが得られています。この計算をブラッシュアップしつつ、次は実験データのないストロンチウム90に取り組んでいます。富樫さんは「奇数の原子核ジルコニウム93やセレン79の計算も進めています。ゆくゆくはセシウムやヨウ素をやりたいです」と話します。
似たような計算を行うには、平均場近似による方法がありますが、核子の数が偶数の核にしか使えません。長寿命核分裂生成物では奇数核が多いので、殻模型計算が向いているのです。さらに大規模な計算を必要とするので、モンテカルロ殻模型でなければ、長寿命核分裂生成物の計算には挑戦できないでしょう。
「原子核は未知なことが多いので、教科書を書き換えることのできる分野だと大学時代に先生から言われたのが、原子核の分野に進んだきっかけです」と話す富樫さん。核変換反応を実現するために、富樫さんの研究成果はおおいに期待されています。2020年度から始まる、さらに大型のスパコンを使ったポスト「京」重点課題にも選ばれ、研究も一層加速することでしょう。富樫さんの研究成果が教科書に加わる日が来るに違いありません。