Just one month after obtaining his PhD in quantum chromodynamics (QCD) from Pisa University in Italy, Guido Cossu was on his way to Japan to carry out post-doctoral work for a KEK Lattice QCD research group. That was three years ago. The program ended in April, only for Cossu to be immediately offered the opportunity to continue his research in a new five-year program helping a different support group connected with the High Performance Computing Infrastructure (HPCI) program that is investigating a number of fields in fundamental science. He readily agreed.
“I was interested in Japan, its culture, before coming here,” says Cossu. “Japan is also a leader in supercomputers, and the HPCI program means I can continue my post-doctoral work as a theoretical physicist in Lattice QCD using supercomputers like the K computer.”
Before attempting to explain Lattice QCD, we first need to grasp what quantum chromodynamics is all about.
QCD is a field theory explaining the strong nuclear force: the interaction between quarks and the gluons that bind these fundamental particles together, and which in turn keep the nucleus of atoms intact. Historically, the theory was used to describe ordinary matter: namely how protons and neutrons interact. Over time it has evolved and today it is used to describe the quark-gluon interactions that take place during high-energy experiments in accelerators, experiments that can weaken the binding forces enough that the interactions can be analyzed by applying the equations of QCD in their simplest form.
We can think of QCD as an expanded version of the simpler to understand quantum electrodynamics (QED): the quantum theory of the electromagnetic force. QED is used to visualize the interaction between charged particles, two electrons, for instance, as an exchange of forces in the form of virtual photons—virtual because they appear briefly only during the exchange process and immediately decay into other particles.
In QED there is only one charge, with a value of positive or negative, charge or anticharge, to consider. But to explain the behavior of quarks in QCD theory, there needs to be three kinds of charges and their corresponding anticharges binding these particles together via gluons. These charges are whimsically designated by colors—red, green and blue—hence the name “chromo”, Greek for color, though the charges have nothing to do with actual colors. The quarks interact with each other by exchanging gluons that carry the color charges. This is in contrast to the QED force carries, the photons, which are chargeless.
Quarks are designated by colors (red, green and blue) and anti-quarks are designated by their additive complementary colors (cyan, magenta and yellow, respectively). However, the particles that different combinations of quarks make up are colorless, for the color combinations of the quarks cancel each other out, much as red, green and blue light combine to form white.
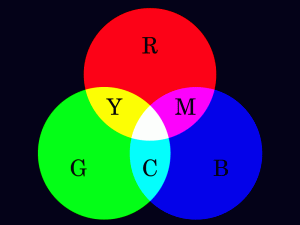
Quarks are designated by colors (red, green and blue) and anti-quarks are designated by their additive complementary colors (cyan, magenta and yellow, respectively). However, the particles that different combinations of quarks make up are colorless, for the color combinations of the quarks cancel each other out, much as red, green and blue light combine to form white.
Yet though QCD is applied to a number of interactions resulting from high-energy particle experiments in accelerators to make sense of the complexity of these interactions, “It is all but impossible to use QCD equations to do the same at low energies, where the couplings are tight, because there are just too many possibilities to consider calculating,” says Cossu.
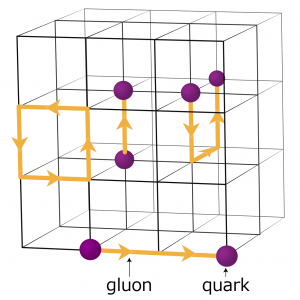
So researches have turned to using computer simulations for help. They have replaced continuous space-time with a more manageable four-dimensional lattice or grid of equally spaced points connected by intersecting lines to represent the three dimensions of space and the dimension of time. Values for quarks are positioned on the crosspoints of the grid, while the lines between them represent the gluon fields. “In effect, we discretize our QCD equations by putting them onto a lattice,” says Cossu.
The computer then completes a series of snapshots of QCD fields, until statistically valid averages are produced of particle decay rates or particle masses. This enables physicists to make predictions about the particle interactions, which can then be compared to measurements obtained in accelerator experiments. The number of calculations required to create such a simulation is enormous and can rise into the billions, for which supercomputers providing teraflops of processing power are required.
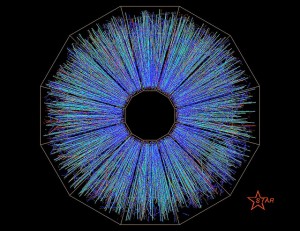
“Specifically, I’m using Lattice QCD to simulate what happens when you heat up particles inserted into a heat box,” says Cossu. By increasing the temperatures beyond 160- megaelectron volts (MeV) (an exceedingly hot temperature when you consider that room temperature is just one-fortieth of one electron volt) you break the normally tight quark-quark couplings known as confinement, and a phase transition into a new state of matter takes place. At this point, the quarks and gluons behave almost as though they are free in a sort of primordial quark-gluon plasma, such as was created at the time of the Big Bang, and before other types of particle came into being.
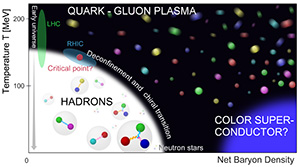
Theoretical diagram based on Lattice QCD simulations depicting expected quark-gluon phase transition.
“And this is exactly what Lattice QCD predicted would happen,” explains Cossu. “But what I’m investigating is why we have confinement at all. Although we have many theories describing the phenomenology of confinement, we can’t explain why quarks are confined.”
In search of the answer, Cossu is using Lattice QCD to study what actually changes during the transition phase—the changes of symmetries among different quarks for example, or the changes in the thermodynamical properties of the matter.
“This is really interesting because when you have changes in the state of matter, you can really see what is happening,” says Cossu. “Then you can trace these changes back, and this gives you an understanding of the properties of the matter in the two phases.”
To carry out his calculations Cossu has been using the IBM Blue Gene/Q supercomputer at KEK, and now his research group has applied to use the more advanced K computer. Programming these high performance supercomputers is another important requirement of Cossu’s work. Because they consist of massively parallel processing cores, they have to be optimized differently for different kinds of calculations. Cossu notes that it’s almost always necessary to redesign previously used algorithms, because what can still work well on several cores, may not be good enough to work well across hundreds of cores. Similarly, distributed memory arranged in a series of hierarchies is the order of the day for these systems, so to be able to make efficient use of supercomputer time, the workload has to be balanced across these hierarchies as equitably as possible.
“For the past six months,” says Cossu, “I’ve been doing this kind of optimization work and also collaborating with researchers at Tsukuba University and Nagoya University to write a common code for Lattice QCD that will be made available to everyone in the lattice community who wants to use it.”
The code they have been using to discretize the theory until now has been written in the Fortran programming language, but this is considered out-dated, so the collaborators have switched to C++. There are many ways to discretize the Lattice QCD theory and different researchers have different ways of working, so C++ will provide the flexibility to accommodate all these requirements.
Also as part of his work for the research support group of the Joint Institute for Computational Fundamental Science (JICFuS) and HPCI Strategic Program (Field 5), Cossu recently published a report on simulating QCD at finite temperatures employing cost-effective graphics processing units. These GPUs are used in personal computers as graphical co-processors, and are the main processor used in video game consoles. Because they can work in parallel, they have proved an economical substitute in place of supercomputers among small groups of researchers.